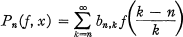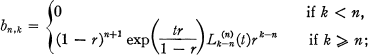Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jakimovski, Amnon
1966.
Summability of the Heine and Neumann Series of Legendre Polynomials.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
1261.
Powell, Robert E.
1967.
Theℐ(r n) summability transform.
Journal d'Analyse Mathématique,
Vol. 20,
Issue. 1,
p.
289.
Swaminathan, V.
1976.
A note on the Valiron method of summability.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 28,
Issue. 3-4,
p.
211.
Kangro, G. F.
1976.
Theory of summability of sequences and series.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 1,
p.
1.