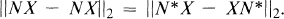Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T02:08:16.941Z Has data issue: false hasContentIssue false
  • English
  • Français

The Metric Fuglede Property and Normality

Published online by Cambridge University Press:  20 November 2018

R. L. Moore  and
G. Weiss
R. L. Moore
Affiliation:
University of Alabama, University, Alabama
G. Weiss
Affiliation:
University of Michigan, Ann Arbor, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4], H. Kamowitz considered the condition, to be satisfied by a bounded operator N on a Hilbert space 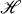, that

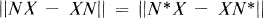
for all operators X on 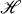. Kamowitz discovered that such an N must be normal and its spectrum must lie on a line or a circle; that is, N must be of the form αJ + β, where α and β are complex numbers and J is either Hermitian or unitary. G. Weiss [5] showed that the Hilbert-Schmidt norm behaves differently: N need only be normal in order that

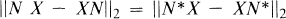
for all finite-rank operators X, and in fact this condition is equivalent to normality. Actually, the result in [5] removes the restriction that X be finite-rank, that is, if N is normal and X is any bounded operator, then

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 516 - 525
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Furuta, T., An extension of the Fuglede-Putnam theorem to subnormal operators using a Hilbert-Schmidt norm inequality, Proc. A.M.S. 81 (1981), 240–242.Google Scholar
2. Gohberg, I. C. and Krein, M. G., Introduction to the theory of linear non-self adjoint operators in Hilbert space, Transi. Math. Monographs 18 (Amer. Math. Soc, Providence, R. I., 1970).Google Scholar
3. Guichardet, A., Tensor products of C*-algebras, Matematisk Institut Lecture note series, Aarhus Universitet (1969).Google Scholar
4. Kamowitz, H., On operators whose spectrum lies on a circle or a line, Pac. J. Math. 20 ( 1967), 65–68.Google Scholar
5. Weiss, G., The Fuglede commutativity theorem modulo the Hilhert-Schmidt class and generating functions for matrix operators II, Journal of Operator Theory 5 (1981), 3–16.Google Scholar