Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:38:37.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Normality Versus Paracompactness inLocally Compact Spaces

Published online by Cambridge University Press:  20 November 2018

Alan Dow  and
Franklin D. Tall
Alan Dow
Affiliation:
Department of Mathematics and Statistics, University of North Carolina, Charlotte, North Carolina 28223, USA e-mail: adow@uncc.edu
Franklin D. Tall
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON MSS 2E4 e-mail: f.tall@math.utoronto.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note provides a correct proof of the result claimed by the second author that locally compact normal spaces are collectionwise Hausdorff in certain models obtained by forcing with a coherent Souslin tree. A novel feature of the proof is the use of saturation of the non-stationary ideal on 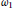${{\omega }_{1}}$, as well as of a strong form of Chang's Conjecture. Together with other improvements, this enables the consistent characterization of locally compact hereditarily paracompact spaces as those locally compact, hereditarily normal spaces that do not include a copy of 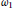${{\omega }_{1}}$.

Keywords

54A3554D2054D4503E3503E5003E5503E57normalparacompactlocally compactcountably tightcollectionwise Hausdorffforcing with a coherent Souslin treeMartin's MaximumPFA(S)[S]Axiom Rmoving off property
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 74 - 96
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Arhangel'skiĭ, A. V., Bicompacta that satisfy the Suslin condition hereditarily. Tightness and free sequences. Dokl. Akad. Nauk SSSR 199(1971), 1227–1230.Google Scholar
[2] Arhangel'skiĭ, A. V., The property ofparacompactness in the class of perfectly normal locally bicompact spaces. Dokl. Akad. Nauk SSSR 203(1972), 1231–1234.Google Scholar
[3] Balogh, Z. T., Locally nice spaces under Martin's axiom. Comment. Math. Univ. Carolin. 24(1983), 63–87.Google Scholar
[4] Balogh, Z. T., Locally nice spaces and axiom R. Topology Appl. 125(2002), 335–341. http://dx.doi.Org/10.1016/S0166-8641 (01)00286-3 Google Scholar
[5] Balogh, Z. T., Dow, A., Fremlin, D. H. , and Nyikos, P. J., Countable tightness and proper forcing. Bull. Amer. Math. Soc. 19(1988), 295–298.http://dx.doi.org/10.1090/S0273-0979-1988-15649-2 Google Scholar
[6] Balogh, Z. T., and Rudin, M. E., Monotone normality, m Topology Appl. 47(1992), 115–127. http://dx.doi.Org/10.1016/0166-8641(92)90066-9 Google Scholar
[7] van Douwen, E. K., A technique for constructing honest locally compact submetrizable examples. Topology Appl. 47(1992), 179–201.http://dx.doi.org/10.101 6/0166-8641(92)90029-Y Google Scholar
[8] Dow, A., On the consistency of the Moore-Mrowka solution. In: Proceedings of the Symposium on General Topology and Applications (Oxford, 1989). Topology Appl. 44(1992), 125–141. http://dx.doi.Org/10.1016/0166-8641 (92)900875-E Google Scholar
[9] Dow, A., Set-theoretic update on topology. In: Recent Progress in General Topology III (Prague, 2011),Atlantis Press, Paris, 2014, pp. 329–357.http://dx.doi.Org/10.2991/978-94-6239-024-9_7 Google Scholar
[10] Dow, A. and Tall, E.D., Hereditarily normal manifolds of dimension > may all be metrizable. http://math2.uncc.edu/-adow/hnjul201 6.pdf +may+all+be+metrizable.+http://math2.uncc.edu/-adow/hnjul201+6.pdf>Google Scholar
[11] Dow, A. and Tall, E.D., PFA(S)[S] and countably compact spaces. Topology Appl. to appear. Google Scholar
[12] Eisworth, T. and Nyikos, P. J., Antidiamond principles and topological applications. Trans. Amer. Math. Soc. 361(2009), 5695–5719.http://dx.doi.org/10.1090/S0002-9947-09-04705-9 Google Scholar
[13] Engelking, R., R General topology. Second ed., Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[14] Feng, Q. and Jech, T., T. Projective stationary sets and a strong reflection principle. J. London Math. Soc. (2) 58(1998), 271–283. http://dx.doi.Org/10.1112/S0024610798006462 Google Scholar
[15] Fischer, A. J., Tall, F. D., and Todorcevic, S., Forcing with a coherent Souslin tree and locally countable subspaces of countably tight compact spaces. Topology Appl. 195(2015), 284–296.http://dx.doi.Org/10.1016/j.topol.2015.09.035 Google Scholar
[16] Fleissner, W. G., Normal Moore spaces in the constructible universe. Proc. Amer. Math. Soc. 46(1974), 294–298.http://dx.doi.org/10.1090/S0002-9939-1974-0362240-4 Google Scholar
[17] Fleissner, W. G., Left separated spaces with point-countable bases. Trans. Amer. Math. Soc. 294(1986), 665–677. http://dx.doi.org/10.1090/S0002-9947-1986-0825729-X Google Scholar
[18] Foreman, M., Magidor, M., and Shelah, S., Martin's maximum, saturated ideals and nonregular ultrafilters I. Ann. of Math. 127(1988), 1–47.http://dx.doi.Org/10.2307/1971415 Google Scholar
[19] Good, C., Large cardinals and small Dowker spaces. Proc. Amer. Math. Soc. 123(1995), 263–272.http://dx.doi.org/10.1090/S0002-9939-1995-1216813-0 Google Scholar
[20] Gruenhage, G. and Koszmider, P., The Arkhangel'skii-Tall problem under Martin's axiom. Fund. Math. 149(1996), 275–285.Google Scholar
[21] Gruenhage, G. and Ma, D., Baireness ofCk (X) for locally compact X. Topology Appl. 80(1997), 131–139.http://dx.doi.Org/10.1016/S0166-8641 (96)00163-0 Google Scholar
[22] Ismail, M. and Nyikos, P., On spaces in which countably compact subsets are closed, and hereditary properties. Topology Appl. 11(1980), 281–292.http://dx.doi.Org/10.1016/0166-8641 (80)90027-9 Google Scholar
[23] Jech, T., Stationary sets. In: Handbook of set theory, Springer, Amsterdam, 2010, pp. 93–128.Google Scholar
[24] Larson, P., An variation for one Souslin tree. J. Symbolic Logic 64(1999), 81–98. http://dx.doi.org/10.2307/2586753 Google Scholar
[25] Larson, P., Martin's maximum and the Pmax axiom. Ann. Pure Appl. Logic 106(2000), 135–149. http://dx.doi.org/10.1016/S01 68-0072(00)00020-8 Google Scholar
[26] Larson, P. and Tall, F. D., Locally compact perfectly normal spaces may all be paracompact. Fund. Math. 210(2010), 285–300.http://dx.doi.org/10.4064/fm210-3-4 Google Scholar
[27] Larson, P. and Tall, F. D., On the hereditary paracompactness of locally compact hereditarily normal spaces. Canad. Math. Bull. 57(2014), 579–584. http://dx.doi.Org/10.4153/CMB-2O14-010-3 Google Scholar
[28] Larson, P. and Todorcevic, S., Katětov's problem. Trans. Amer. Math. Soc. 354(2002), 1783–1791. http://dx.doi.org/10.1090/S0002-9947-01-02936-1 Google Scholar
[29] Laver, R., Making the supercompactness ofu indestructible under K-directed closed forcing. Israel J. Math. 29(1978), 385–388.http://dx.doi.Org/10.1007/BF02761175 Google Scholar
[30] McCoy, R. A. and Ntantu, I., Topological properties of spaces of continuous functions. Lecture Notes in Mathatics, 1315, Springer-Verlag, Berlin, 1988.http://dx.doi.Org/10.1007/BFb0098389 Google Scholar
[31] Miyamoto, T., On iterating semiproper preorders. J. Symbolic Logic 67(2002), 1431–1468.http://dx.doi.Org/10.2178/jsl/11901 50293 Google Scholar
[32] Nyikos, P. J., Crowding of functions, para-saturation of ideals, and topological applications. Topology Proc. 28(2004), 241–246.Google Scholar
[33] Porter, J. and Woods, R., Extensions and absolutes of Hausdorff spaces. Springer-Verlag, New York,1988.http://dx.doi.Org/10.1007/978-1-4612-3712-9 Google Scholar
[34] Shelah, S., Proper and improper forcing. Second ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998. http://dx.doi.org/10.1007/978-3-662-12831-2 Google Scholar
[35] Szentmiklossy, Z., S-Spaces and L-spaces under Martin's Axiom. Coll. Math. Soc. Janes Bolyai, 23, North-Holland, Amsterdam, 1980, pp. 1139–1145.Google Scholar
[36] Tall, F. D., Set-theoretic consistency results and topological theorems concerning the normal Moore space conjecture and related problems. Dissertationes Math. (Rozprawy Mat.) 148(1977), 1–53.Google Scholar
[37] Tall, F. D., Covering and separation properties in the Easton model. Topology Appl. 28(1988), 155–163.http://dx.doi.Org/10.1016/0166-8641 (88)90007-7 Google Scholar
[38] Tall, F. D., PFA(S)[S]and the Arhangel'skiĭ-Tall problem. Topology Proc. 40(2012), 99–120.Google Scholar
[39] Tall, F. D., PFA(S)[S]: more mutually consistent topological consequences of PFA and V == L. Canad. J. Math. 64(2012), 1182–1200.http://dx.doi.Org/10.4153/CJM-2O12-010-0 Google Scholar
[40] Tall, F. D., PFA(S)[S]and locally compact normal spaces. Topology Appl. 162(2014), 100–115.http://dx.doi.Org/10.1016/j.topol.2013.11.012 Google Scholar
[41] Tall, F. D., Some observations on the Baireness of Ck(X) for a locally compact space X. Topology Appl. 213(2016), 212–219.http://dx.doi.Org/10.1016/j.topol.2016.08.021 Google Scholar
[42] Tall, F. D., PFA(S)[S]for the masses. Topology Appl. to appear. Google Scholar
[43] Todorcevic, S., Directed sets and cofinal types. Trans. Amer. Math. Soc. 290(1985), 711–723.http://dx.doi.org/10.1090/S0002-9947-1985-0792822-9 Google Scholar
[44] Todorcevic, S., Walks on ordinals and their characteristics. Progress in Mathematics, 263, Birkhäuser Verlag, Basel, 2007.Google Scholar
[45] Todorcevic, S., Forcing with a coherent Souslin tree, preprint, 2010.http://www.math.toronto.edu/~stevo/todorcevic_chain_cond.pdf Google Scholar
[46] Watson, W. S., Locally compact normal spaces in the constructible universe. Canad. J. Math. 34(1982), 1091–1096.http://dx.doi.org/10.4153/CJM-1982-078-8 Google Scholar
[47] Woodin, W.H., The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter Series in Logic and its Applications, 1, Walter de Gruyter & Co., Berlin, 1999.http://dx.doi.org/10.1515/9783110804737 Google Scholar