Article contents
On Open Projections of GCR Algebras
Published online by Cambridge University Press: 20 November 2018
Extract
Throughout this paper 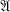 will denote a C*-algebra and
will denote a C*-algebra and 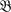 will denote its second dual, which is identified with the enveloping von Neumann algebra of
will denote its second dual, which is identified with the enveloping von Neumann algebra of 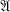 . A projection E in
. A projection E in 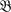 is said to be open if it supports a left ideal in
is said to be open if it supports a left ideal in 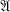 , that is, if
, that is, if 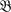 E =
E = 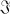 - for some left ideal
- for some left ideal 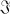 in
in 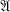 . Here the bar - means the stong closure. When
. Here the bar - means the stong closure. When 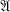 has a unit, this definition coincides with the definition of Akemann [1, Definition II. 1]. In the sequel, we shall solely be concerned with two-sided ideals, and consequently central projections [4, I, § 3, Corollary 3 of Theorem 2]. Our aim is to show that
has a unit, this definition coincides with the definition of Akemann [1, Definition II. 1]. In the sequel, we shall solely be concerned with two-sided ideals, and consequently central projections [4, I, § 3, Corollary 3 of Theorem 2]. Our aim is to show that 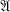 is CCR if and only if the open central projections are strongly dense in the set of central projections on
is CCR if and only if the open central projections are strongly dense in the set of central projections on 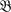 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
- 2
- Cited by

