Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T10:07:49.975Z Has data issue: false hasContentIssue false
  • English
  • Français

On Periodicity in Topological Surgery

Published online by Cambridge University Press:  20 November 2018

Slawomir Kwasik
Slawomir Kwasik*
Affiliation:
University of Oklahoma, Norman, Oklahoma
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the distinguishing features of the topological category is the following periodicity in the set of homotopy TOP structures on X.

THEOREM (Siebenmann). Let Xm, m ≦ 5, be a connected compact topological manifold with non-empty boundary. Then

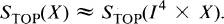
It was conjectured by Siebenmann (see [3], p. 283) that the analogous periodicity should also exist for noncompact manifolds.

The purpose of this paper is to prove that this is indeed the case, namely:

THEOREM 1. Let Let Xm, m ≦ 6, be a connected noncompact topological manifold with non-empty boundary. Then

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1053 - 1064
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Farrell, F. T. and Wagoner, J. B., Infinite matrices in algebraic K-theory and topology, Comm. Math. Helv. 47 (1972), 474–501.Google Scholar
2. Farrell, F. T., Taylor, L. R. and Wagoner, J. B., The Whitehead theorem in proper category, Comp. Math. 27 (1971), 1–23.Google Scholar
3. Kirby, R. C. and Siebenmann, L. C., Foundational essays on topological manifolds, smoothings, and triangulations, Annals of Math. Studies 88 (Princeton University Press, Princeton, 1977).CrossRefGoogle Scholar
4. Maumary, S., Proper surgery groups for non-compact manifolds of finite dimension, preprint, Berkeley (1972).Google Scholar
5. Maumary, S., Proper surgery groups and Wall-Novikov groups, Proc. of the Battelle Seattle Conf. on Algebraic K-theory, Springer Lecture Notes 343 (1913), 526–539.Google Scholar
6. Nicas, A., Induction theorems for groups of homotopy manifold structures, Mem. Amer. Math. Soc. 267 (1982).Google Scholar
7. Quinn, F., A geometric formulation of surgery, in Topology of manifolds (Markham, Chicago, 1970), 500–511.Google Scholar
8. Ranicki, A., On algebraic L-theory, I: Foundations, Proc. London Math. Soc. 27 (1973), 101–125.Google Scholar
9. Ranicki, A., The algebraic theory of surgery II. Applications to topology, Proc. London Math. Soc. 43 (1980), 193–283.Google Scholar
10. Rourke, C. P. and Sanderson, B.J., Δ-sets I, Quart. J. Math. Oxford, 222 (1971), 321–338.Google Scholar
11. Shaneson, J. L., WalVs surgery obstruction groups for G × Z, Ann. of Math. 90 (1969), 296–334.Google Scholar
12. Siebenmann, L. C., Infinite simple homotopy types, Indag. Math. 32 (1970), 479–495.Google Scholar
13. Taylor, L. R., Surgery on paracompact manifolds, Berkeley Ph.D. Thesis (1972).Google Scholar
14. Wall, C. T. C., Surgery on compact manifolds (Academic Press, London, 1970).Google Scholar