Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:40:43.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On Positive Definite Functions over a Locally Compact Group

Published online by Cambridge University Press:  20 November 2018

J. F. Price
J. F. Price*
Affiliation:
The Australian National University, Canberray Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we are concerned with several questions on positive definite functions over a Hausdorff locally compact group. The main result, Theorem A, gives some necessary and sufficient conditions for to be a positive definite function when μ is a (complex Radon) measure. In particular, is a positive definite function if and only if μ ∊ L2, and Theorem B then follows by giving a complete characterization of functions of the type 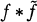, where f ∊ L2. Perhaps the most interesting aspect of these results is that they provide further examples of results over a non-abelian, non-compact group, which otherwise are simple consequences (with μ, a bounded measure in Theorem A) of the theorems of Plancherel and Bochner.

Unless otherwise specified, all notation and definitions will follow [1;2]. The underlying group will always be G, a Hausdorff locally compact group with identity e, and with left Haar measure dx.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 892 - 896
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Dixmier, J., Les algèbres d'opérateurs dans l'espace Hilbertien (Gauthier-Villars, Paris, 1957).Google Scholar
2. Edwards, R. E., Functional analysis: Theory and applications (Holt, Rinehart, and Winston, Inc., New York, 1965).Google Scholar
3. Eymard, P., Valgèbre de Fourier d'un groupe localement compact, Bull. Soc. Math. France 92 (1964), 181–236.Google Scholar
4. Hewitt, E. and Ross, K. A., Abstract harmonic analysis, Vol. I (Springer-Verlag, Berlin, 1963).Google Scholar