Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T02:04:41.194Z Has data issue: false hasContentIssue false
  • English
  • Français

On Varieties of Lie Algebras of Maximal Class

Published online by Cambridge University Press:  20 November 2018

Tatyana Barron ,
Dmitry Kerner  and
Marina Tvalavadze
Tatyana Barron
Affiliation:
Department of Mathematics, University of Western Ontario, LondonON N6A 5B7. e-mail: tatyana.barron@uwo.ca
Dmitry Kerner
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, P.O.B. 653, Be'er Sheva 84105, Israel. e-mail: dmitry.kerner@gmail.com
Marina Tvalavadze
Affiliation:
Fields Institute for Research in Mathematical Sciences, TorontoON, M5T 3J1. e-mail: mtvalava@fields.utoronto.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study complex projective varieties that parametrize (finite-dimensional) filiform Lie algebras over 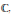$\mathbb{C}$ using equations derived by Millionshchikov. In the infinite-dimensional case we concentrate our attention on 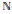$\mathbb{N}$-graded Lie algebras of maximal class. As shown by $\text{A}$. Fialowski there are only three isomorphism types of 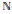$\mathbb{N}$-graded Lie algebras 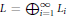$L\,=\,\oplus _{i=1}^{\infty }\,{{L}_{i}}$ of maximal class generated by ${{L}_{i}}$ and 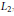${{L}_{2}}$, 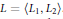$L\,=\,\left\langle {{L}_{1}},\,{{L}_{2}} \right\rangle$. Vergne described the structure of these algebras with the property $L\,=\,\left\langle {{L}_{1}} \right\rangle$. In this paper we study those generated by the first and $q$-th components where 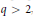$q\,>\,2$, 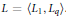$L\,=\,\left\langle {{L}_{1}},\,{{L}_{q}} \right\rangle$. Under some technical condition, there can only be one isomorphism type of such algebras. For 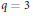$q=\,3$ we fully classify them. This gives a partial answer to a question posed by Millionshchikov.

Keywords

17B7014F45filiform Lie algebrasgraded Lie algebrasprojective varietiestopologyclassification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 55 - 89
Copyright
Copyright © Canadian Mathematical Society 2015

References

[B] Bratzlavsky, F.. Classification des algèbras de Lie nilpotentes de dimension n, de classe n – 1, dont l’idéal dérivé est commutatif. Acad. Roy. Belg. Bull. Cl. Sci. 60(1974), 858–865.Google Scholar
[CGS] Ciralo, S., de Graaf, W. A., and Schneider, C., Six-dimensional nilpotent Lie algebras. Linear Algebra Appl. 436(2012), no. 1, 163–189. http://dx.doi.org/10.1016/j.laa.2011.06.037 Google Scholar
[D] Dimca, A., Singularities and topology of hypersurfaces. Universitext, Springer-Verlag, New York, 1992.Google Scholar
[ENR] Echarte, F. J., Núñez, J. and Ramírez, F., Description of some families of filiform Lie algebras. Houston J. Math. 34(2008), no. 1, 19–32.Google Scholar
[F] Fialowski, A., On the classification of graded Lie algebras with two generators. (Russian) Vestnik Moskov. Univ. Ser. I Mat. Mekh. 1983, no. 2, 62–64.Google Scholar
[FF] Fomenko, A. T. and Fuks, D. B., Kurs gomotopicheskoi topologii. (Russian) [A course in homotopic topology] “Nauka”, Moscow, 1989.Google Scholar
[G] Gong, M.-P., Classification of nilpotent Lie algebras of dimension 7 (over algebraically closed fields and R). Ph.D. thesis, University of Waterloo, 1998.Google Scholar
[GH] Griffiths, P. and Harris, J., Principles of algebraic geometry. JohnWiley & Sons, Inc., New York, 1994.Google Scholar
[Ha] You. Hakimjanov, B., Variété des lois d’algèbres de Lie nilpotentes. Geom. Dedicata 40(1991), no. 3, 269–295.Google Scholar
[Hi] Hirzebruch, F., Topological methods in algebraic geometry. Third enlarged ed., Springer-Verlag New York, Inc., New York, 1966.Google Scholar
[KN] Kirillov, A. and Neretin, Yu., The variety An of n-dimensional Lie algebra structures. In: Some problems in modern analysis, Fourteen papers translated from Russian. AMS Transl., Ser. 2, 137, 1987, 21–30.Google Scholar
[L] Löfwall, C., Solvable infinite filiform Lie algebras J. Commut. Algebra 2(2010), no. 4., 429–436.http://dx.doi.org/10.1216/JCA-2010-2-4-429 Google Scholar
[M1] Millionshchikov, D., The variety of Lie algebras of maximal class. Proc. Steklov Inst. Math. 266(2009), no. 1, 177–194.Google Scholar
[M2] Millionshchikov, D., Graded filiform Lie algebras and symplectic nilmanifolds. In: Geometry, topology, and mathematical physics, Amer. Math. Soc. Transl. Ser. 2, 212, American Mathematical Society, Providence, RI, 2004, pp. 259–279.Google Scholar
[SZ] Shalev, A. and Zelmanov, E., Narrow Lie algebras: a coclass theory and a characterization of the Witt algebra. J. Algebra 189(1997), no. 2, 294–331. http://dx.doi.org/10.1006/jabr.1996.6819 Google Scholar
[T] Tsagas, Gr., Lie algebras of dimension eight. J. Inst. Math. Comput. Sci. Math. Ser. 12(1999), no. 3, 179–183.Google Scholar
[V] Vergne, M., Cohomologie des algèbres de Lie nilpotentes. Application à l’étude de la variétédes algèbres de Lie nilpotentes. Bull. Soc. Math. France 98(1970), 81–116.Google Scholar