Published online by Cambridge University Press: 20 November 2018
Let
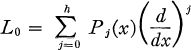
be an ordinary differential operator of order h whose coefficients are (η, η) matrices defined on the interval 0 ≤ x < ∞, hη = n = 2v. Let the operator L0 be formally self adjoint and let v boundary conditions be given at x = 0 such that the eigenvalue problem
(1.1)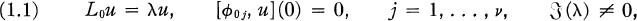
has no non-trivial square integrable solution. This paper deals with the perturbed operator L∈ = L0 + ∈q where ∈ is a real parameter and q(x) is a bounded positive (η, η) matrix operator with piecewise continuous elements 0 ≤ x < ∞. Sufficient conditions involving L0, q are given such that L∈ determines a selfadjoint operator H∈ and such that the spectral measure E∈(Δ′) corresponding to H∈ is an analytic function of ∈, where Δ′ is a subset of a fixed bounded interval Δ = [α, β]. The results include and improve results obtained for scalar differential operators in an earlier paper (3).