Published online by Cambridge University Press: 20 November 2018
In [3] Lissner defined a class of rings called outer product rings, (OP-rings). These are commutative rings R with identity for which every exterior vector 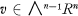 is decomposable, i.e.,
is decomposable, i.e., 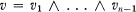 with
with 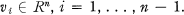 .
.
If we look only at those vectors 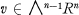 whose co-ordinates with respect to any basis of
whose co-ordinates with respect to any basis of 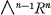 generate the unit ideal in R and consider those rings R for which all vectors of this type are decomposable, we obtain the class of rings which have been referred to as Her mite-rings (H-rings, see also Lissner [3]). This class of H-rings evidently contains the class of OP-rings.
generate the unit ideal in R and consider those rings R for which all vectors of this type are decomposable, we obtain the class of rings which have been referred to as Her mite-rings (H-rings, see also Lissner [3]). This class of H-rings evidently contains the class of OP-rings.