No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Given a homotopy class [f] in πn(X), we say that [f] is projective if and only if there is a homotopy commutative factorization
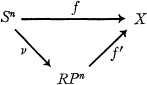
where v is the standard double covering. We then denote by 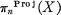 the subset of projective homotopy classes in πn(X).
the subset of projective homotopy classes in πn(X).
The notion of projective homotopy classes was studied in the author's thesis [5], and the projective homotopy classes for spheres in the stable range, up through the 3-stem were calculated in [6].