Article contents
Separating Closed Sets by Continuous Mappings into Developable Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
A topological space X is called developable if it has a development, i.e., a sequence 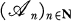 of open covers of X such that for each x ∈ X the collection
of open covers of X such that for each x ∈ X the collection 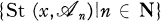 is a neighbourhood base of x, where
is a neighbourhood base of x, where
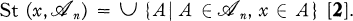
This class of spaces has turned out to be one of the most natural and useful generalizations of metrizable spaces [23]. In [4] it was shown that some well known results in metrization theory have counterparts in the theory of developable spaces (i.e., Urysohn's metrization theorem, the Nagata-Smirnov theorem, and Nagata's “double sequence theorem”). Moreover, in [3] it was pointed out that subspaces of products of developable spaces (i.e., D-completely regular spaces) can be characterized in much the same way as subspaces of products of metrizable spaces (i.e., completely regular T1-spaces).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 7
- Cited by


