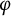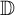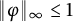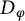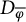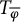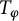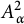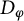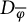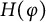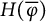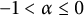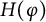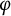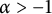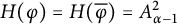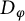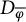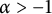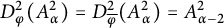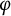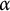Sub-Bergman Hilbert spaces on the unit disk III

Abstract

For a bounded analytic function $\varphi $ on the unit disk $\mathbb {D}$ with $\|\varphi \|_\infty \le 1$, we consider the defect operators $D_\varphi $ and $D_{\overline \varphi }$ of the Toeplitz operators $T_{\overline \varphi }$ and $T_\varphi $, respectively, on the weighted Bergman space $A^2_\alpha $. The ranges of $D_\varphi $ and $D_{\overline \varphi }$, written as $H(\varphi )$ and $H(\overline \varphi )$ and equipped with appropriate inner products, are called sub-Bergman spaces.

We prove the following three results in the paper: for $-1<\alpha \le 0$, the space $H(\varphi )$ has a complete Nevanlinna–Pick kernel if and only if $\varphi $ is a Möbius map; for $\alpha>-1$, we have $H(\varphi )=H(\overline \varphi )=A^2_{\alpha -1}$ if and only if the defect operators $D_\varphi $ and $D_{\overline \varphi }$ are compact; and for $\alpha>-1$, we have $D^2_\varphi (A^2_\alpha )= D^2_{\overline \varphi }(A^2_\alpha )=A^2_{\alpha -2}$ if and only if $\varphi $ is a finite Blaschke product. In some sense, our restrictions on $\alpha $ here are best possible.

1 Introduction

Let $\mathcal {H}$ be a Hilbert space, and let $B(\mathcal {H})$ be the space of all bounded linear operators on $\mathcal {H}$ . If $T\in B(\mathcal {H})$ is a contraction, we use $H(T)$ to denote the range space of the defect operator $(I-TT^*)^{1/2}$ . It is well known that $H(T)$ is a Hilbert space with the inner product

$$ \begin{align*}\langle (I-TT^*)^{1/2} x, (I-TT^*)^{1/2}y\rangle_{H(T)} = \langle x, y\rangle_{\mathcal{H}},\end{align*} $$

where $x, y \in \mathcal {H} \ominus \ker (I-TT^*)^{1/2}$ . Spaces of the type $H(T)$ have been studied extensively in the literature, mostly in connection with operator models.

There are two special cases that are especially interesting. First, if $\mathcal {H}=H^2$ is the classical Hardy space on the unit disk $\mathbb {D}$ , and if $T=T_\varphi $ is the analytic Toeplitz operator (multiplication operator) induced by a function $\varphi $ in the unit ball $H^\infty _1$ of $H^\infty $ , then $H(T_\varphi )$ is called a sub-Hardy space (or a de Branges–Rovnyak space). Such spaces appeared in the work [11] of de Branges concerning the Bieberbach conjecture and were studied systematically in Sarason’s monograph [21]. See also the recent monograph [12].

Second, if $\mathcal {H}=A^2$ is the classical Bergman space on the unit disk and if $T=T_\varphi $ is the analytic Toeplitz operator (multiplication operator) on $A^2$ for some $\varphi \in H^\infty _1$ , then $H(T_\varphi )$ is naturally called a sub-Bergman space. Such spaces have been studied by several authors in the literature, beginning with [25, 26] and including [1, 8–10, 13, 14, 18, 20, 22, 23].

In this paper, we focus on sub-Bergman spaces in the weighted case. More specifically, we will consider a family of “generalized Bergman spaces” $A^2_\alpha $ . With the definition of generalized Bergman spaces $A^2_\alpha $ deferred to the next section, we mention the following special cases: $A^2_0=A^2$ is the ordinary Bergman space, $A^2_{-1}=H^2$ is the Hardy space, and $A^2_{-2}=\mathcal {D}$ is the Dirichlet space. We will also consider multiplications operators $T_\varphi =T_\varphi ^\alpha : A^2_\alpha \to A^2_\alpha $ induced by functions from $\mathcal {M}_1(A^2_\alpha )$ , the closed unit ball of the multiplier algebra $\mathcal {M}(A^2_\alpha )$ of $A^2_\alpha $ . It is natural for us to use the notation $H^\alpha (\varphi )$ for the space $H(T_\varphi )$ . Similarly, we will write $H^\alpha (\overline \varphi )$ for the space $H(T)$ when T is the adjoint operator $T^*_\varphi : A^2_\alpha \to A^2_\alpha $ . Note that for $\alpha \ge -1$ , we have $\mathcal {M}(A^2_\alpha )=H^\infty $ .

Motivated by the main results obtained in [10, 26], we will study the following three problems:

1. (a) When does $H^\alpha (\varphi )$ have a complete Nevanlinna–Pick (CNP) kernel?

2. (b) When do we have $H^\alpha (\varphi )=H^\alpha (\overline \varphi )=A^2_{\alpha -1}$ ?

3. (c) When do we have $(I-T_\varphi T_{\overline \varphi })(A^2_\alpha )=(I-T_{\overline \varphi }T_\varphi )(A^2_\alpha )=A^2_{\alpha -2}$ ?

Our main results are Theorems A–C below.

Theorem A For $-1<\alpha \le 0$ , the space $H^\alpha (\varphi )$ has a CNP kernel if and only if $\varphi $ is a Möbius map. When $\alpha> 0$ , $H^\alpha (\varphi )$ does not have a CNP kernel.

A (more subtle) characterization is also obtained when $-2<\alpha <-1$ . Here, even the result for the case $\alpha =0$ is new. The case $\alpha =-1$ was studied in [10].

Theorem B For $\alpha>-1$ , we have $H^\alpha (\varphi )=H^\alpha (\overline \varphi ) =A^2_{\alpha -1}$ if and only if $\varphi $ is a finite Blaschke product, which is also equivalent to the corresponding defect operators being compact.

Our methods rely on the assumption $\alpha>-1$ in a very critical way. In particular, the result above is definitely invalid when $\alpha =-1$ (the Hardy space case). Some special cases of this result can be found in [1, 8, 9, 14, 22, 26].

Theorem C For $\alpha>-1$ , we have $(I-T_\varphi T_{\overline \varphi })(A^2_\alpha )= (I-T_{\overline \varphi }T_\varphi )(A^2_\alpha )=A^2_{\alpha -2}$ if and only if $\varphi $ is a finite Blaschke product.

The special case $\alpha =0$ was proved in [26]. Once again, the assumption $\alpha>-1$ is critical here.

2 Generalized Bergman spaces

For any real number $\alpha $ , we fix some nonnegative integer k such that $2k+\alpha>-1$ and let $A^2_\alpha $ denote the space of analytic functions f on $\mathbb {D}$ such that

(2.1) $$ \begin{align} \int_{\mathbb{D}}(1-|z|^2)^{2k}|f^{(k)}(z)|^2\,dA_\alpha(z)<\infty, \end{align} $$

where

$$ \begin{align*}dA_\alpha(z)=(1-|z|^2)^\alpha\,dA(z).\end{align*} $$

Here, $dA$ is the normalized area measure on $\mathbb {D}$ . It is easy to see that the weighted area measure $dA_\alpha $ is finite if and only if $\alpha>-1$ , in which case we will normalize $dA_\alpha $ so that $A_\alpha (\mathbb {D})=1$ .

It is well known that the space $A^2_\alpha $ is independent of the choice of the integer k used in (2.1). Two particular examples are worth mentioning: $A^2_{-1}=H^2$ and $A^2_{-2}=\mathcal {D}$ , the Hardy and Dirichlet spaces, respectively. See [24] for more information about the “generalized weighted Bergman spaces” $A^p_\alpha $ .

Each space $A^2_\alpha $ is a Hilbert space with a certain choice of inner product. For example, if $\alpha>-1$ , we can choose $k=0$ in (2.1) and simply use the natural inner product in $L^2(\mathbb {D}, dA_\alpha )$ for $A^2_\alpha $ :

$$ \begin{align*}\langle f,g\rangle=\int_{\mathbb{D}} f(z)\overline{g(z)}\,dA_\alpha(z).\end{align*} $$

More generally, for any $\alpha>-2$ , it is easy to show that an analytic function $f(z)=\sum _{n=0}^\infty a_nz^n$ belongs to $A^2_\alpha $ if and only if

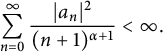$$ \begin{align*}\sum_{n=0}^\infty\frac{|a_n|^2}{(n+1)^{\alpha+1}}<\infty.\end{align*} $$

Since

$$ \begin{align*}\frac{n!}{\Gamma(n+2+\alpha)}\sim\frac1{(n+1)^{\alpha+1}}\end{align*} $$

as $n\to \infty $ , we see that

$$ \begin{align*}\langle f,g\rangle=\sum_{n=0}^\infty\frac{n!\,\Gamma(2+\alpha)}{\Gamma(n+2+\alpha)}\,a_n\overline b_n,\qquad f(z)=\sum_{n=0}^\infty a_nz^n,\quad g(z)=\sum_{n=0}^\infty b_nz^n\end{align*} $$

defines an inner product on $A^2_\alpha $ . With this inner product, the functions

$$ \begin{align*}e_n(z)=\sqrt{\frac{\Gamma(n+2+\alpha)}{n!\,\Gamma(2+\alpha)}}\,z^n,\qquad n\ge0,\end{align*} $$

form an orthonormal basis for $A^2_\alpha $ , which yields the reproducing kernel of $A^2_\alpha $ as follows:

(2.2) $$ \begin{align} K(z,w)=\sum_{n=0}^\infty e_n(z)\overline{e_n(w)}=\sum_{n=0}^\infty\frac{\Gamma(n+2+\alpha)}{n!\,\Gamma(2+\alpha)} \,(z\overline w)^n=\frac1{(1-z\overline w)^{2+\alpha}}. \end{align} $$

Although all spaces $A^2_\alpha $ , when $\alpha>-2$ , have the same type of reproducing kernel as given in (2.2), their multiplier algebras depend on $\alpha $ in a critical way. It is well known that $\mathcal {M}(A^2_\alpha ) =H^\infty $ for $\alpha \ge -1$ . When $\alpha <-1$ , $\mathcal {M}(A^2_\alpha )$ is a proper sub-algebra of $H^\infty $ .

We will consider the defect operators

$$ \begin{align*}D_\varphi = D_\varphi^\alpha = \left(I-T_\varphi T_\varphi^*\right)^{1/2},\qquad D_{\overline\varphi} = D_{\overline\varphi}^\alpha=\left(I-T_\varphi^*T_\varphi\right)^{1/2},\end{align*} $$

and the associated operators

$$ \begin{align*}E_\varphi=E_\varphi^\alpha=I-T_\varphi T_\varphi^*,\qquad E_{\overline\varphi}=E_{\overline\varphi}^\alpha=I-T_\varphi^*T_\varphi,\end{align*} $$

where $\varphi \in \mathcal {M}_1(A^2_\alpha )$ and $T_\varphi : A^2_\alpha \to A^2_\alpha $ is the (contractive) multiplication operator.

Recall that

$$ \begin{align*}H^\alpha(\varphi)=H(T_\varphi),\qquad H^\alpha(\overline\varphi)=H(T^*_\varphi),\end{align*} $$

which are the generalized sub-Bergman Hilbert spaces defined in the Introduction. For any $\alpha>-2$ , just like the unweighted case $\alpha =0$ , $H^\alpha (\varphi )$ is a reproducing kernel Hilbert space whose kernel function is given by

(2.3) $$ \begin{align} K^{\alpha,\varphi}(z,w)=K^{\alpha,\varphi}_w(z)=\frac{1-\varphi(z)\overline{\varphi(w)}}{(1-z\overline w)^{2+\alpha}}. \end{align} $$

Similarly, $H^\alpha (\overline \varphi )$ is a reproducing kernel Hilbert space whose kernel function is given by

$$ \begin{align*} K^{\alpha,\overline\varphi}(z,w)=K^{\alpha,\overline\varphi}_w(z)=\int_{\mathbb{D}}\frac{1-|\varphi(u)|^2} {(1-z\overline u)^{2+\alpha}(1-u\overline w)^{2+\alpha}}\,dA_\alpha(u). \end{align*} $$

The spaces $H^\alpha (\varphi )$ and $H^\alpha (\overline \varphi )$ have been studied by several authors, mostly in the case $\alpha \ge 0$ . See [9, 22] for example. We will generalize several results in the literature to weighted Bergman spaces $A^2_\alpha $ with $\alpha>-1$ .

3 Complete Nevanlinna–Pick kernels

In this section, we will determine exactly when the reproducing kernel function $K_w^{\alpha ,\varphi }$ in (2.3) is a CNP kernel. The following definition is from Theorem 8.2 in [3].

Definition 3.1 Suppose $K=K(z,w)=K_w(z)$ is an irreducible kernel function on a set $\Omega \,$ . K is called a CNP kernel if there are an auxiliary Hilbert space $\mathcal {L}$ , a function $b: \Omega \rightarrow \mathcal {L}$ , and a nowhere vanishing function $\delta $ on $\Omega $ such that

$$ \begin{align*}K_w(z) = \frac{\delta(z) \overline{\delta(w)}}{1-\langle b(z), b(w)\rangle},\qquad z,w\in\Omega.\end{align*} $$

If K is a CNP kernel, the corresponding Hilbert space $\mathcal {H}(K)$ with kernel K is called a CNP space. CNP spaces share many properties with the Hardy space $H^2$ , and they have been studied extensively in the literature (see, e.g., [2, 4–7] and the references therein for recent developments). In 2020, Chu [10] determined which de Branges–Rovnyak spaces (sub-Hardy spaces) have CNP kernel. We will characterize which sub-Bergman spaces have CNP kernel.

The reproducing kernel for the Hardy space $H^2$ is

$$ \begin{align*}K^{H^2}_w(z) = \frac{1}{1-z\overline{w}}.\end{align*} $$

If $\varphi \in H^\infty _1$ is not a constant, we let

$$ \begin{align*}H(K^{H^2}\circ \varphi) = \{f\circ \varphi: f \in H^2\}.\end{align*} $$

Then

$$ \begin{align*}K^{H^2}\circ \varphi(z,w) = K^{H^2}(\varphi(z),\varphi(w)) = \frac{1}{1-\varphi(z)\overline{\varphi(w)}}\end{align*} $$

is a kernel function and $C_\varphi : H^2 \rightarrow H(K^{H^2}\circ \varphi )$ defined by $C_\varphi f = f \circ \varphi $ is a unitary (see [19, p. 71]).

Given $a\in \mathbb {D}$ , we let

$$ \begin{align*}\varphi_a(z) = \frac{a-z}{1-\overline az}\end{align*} $$

denote the Möbius map that interchanges the points $0$ and a. If we take $a=\varphi (0)$ and define

$$ \begin{align*}\psi(z)=\varphi_a(\varphi(z)),\qquad g(z)=\frac{\sqrt{1-|a|^2}}{1-\overline a\varphi(z)},\end{align*} $$

then an easy calculation shows that

(3.1) $$ \begin{align} K^{\alpha,\psi}_w(z)= g(z)\,\overline{g(w)}\,K^{\alpha,\varphi}_w(z). \end{align} $$

See, e.g., [17, p. 18]. So $K^{\alpha ,\varphi }_w(z)$ is a CNP kernel if and only if $K^{\alpha ,\psi }_w(z)$ is a CNP kernel.

The following result can be obtained from [19, Theorem 6.28].

Lemma 3.1 Let $\mathcal {H}_1$ and $\mathcal {H}_2$ be reproducing kernel Hilbert spaces of functions on a set $\Omega $ with reproducing kernels $K_1$ and $K_2$ , respectively. Let $\mathcal {F}$ be a Hilbert space, and let $\Phi : \Omega \rightarrow \mathcal {B}(\mathcal {F},\mathbb {C})$ be a function. Then the following are equivalent:

1. 1. $\Phi $ is a contractive multiplier from $\mathcal {H}_1\otimes \mathcal {F}$ to $\mathcal {H}_2$ .

2. 2. $K_2(z,w)-K_1(z,w)\Phi (z)\Phi (w)^*$ is positive-definite.

We will use $\mathcal {M}_1(\mathcal {H}_1, \mathcal {H}_2)$ to denote the set of contractive multipliers from $\mathcal {H}_1$ to $\mathcal {H}_2$ . When $\mathcal {H}_1=\mathcal {H}_2=\mathcal {H}$ , we will simplify the notation to $\mathcal {M}_1(\mathcal {H})$ .

Lemma 3.2 Let $\varphi \in H^\infty _1$ be a nonconstant function. Then

$$ \begin{align*}\mathcal{M}_1(H(K^{H^2}\circ \varphi)) = \bigl\{f\circ \varphi: f \in \mathcal{M}_1(H^2)\bigr\}.\end{align*} $$

Proof This follows easily from the fact that $C_{\varphi }: H^2 \rightarrow H(K^{H^2}\circ \varphi )$ is a unitary.

In what follows, we will use the notation $K(z,w)\succeq 0$ or $0\preceq K(z,w)$ to mean that $K(z,w)$ is a reproducing kernel, that is, $K(z,w)=\overline {K(w,z)}$ and it is positive-definite in the sense that

$$ \begin{align*}\sum_{i,j=1}^NK(z_i,z_j)c_i\overline c_j\ge0\end{align*} $$

for all $z_i\in \mathbb {D}$ and $c_i\in \mathbb {C}$ , $1\le i\le N$ , and $N\ge 1$ . We will begin with the following result for the ordinary Bergman space, which illustrates the main techniques we use in this section.

Theorem 3.3 Let $\varphi \in H^\infty _1$ and $\alpha =0$ . Then $K^\varphi _w(z)=:K^{0,\varphi }_w(z)$ is a CNP kernel if and only if $\varphi $ is a Möbius map.

Proof If $\varphi $ is a Möbius map, say

$$ \begin{align*}\varphi = \zeta \frac{a-z}{1-\overline az},\qquad \zeta \in \mathbb{T}, a \in \mathbb{D},\end{align*} $$

then it is easy to check that

$$ \begin{align*}K^\varphi_w(z) = \frac{1-|a|^2}{(1-\overline az)(1-a\overline{w})}\frac{1}{1-z\overline{w}},\end{align*} $$

which is clearly a CNP kernel.

Conversely, suppose $K^\varphi _w(z)$ is a CNP kernel. If $a = \varphi (0) \neq 0$ , then we consider $\psi (z)=\varphi _a(\varphi (z))$ . By (3.1), we have that $K^\psi _w(z)$ is a CNP kernel and $\psi (0) = 0$ . So we will assume that $\varphi $ also satisfies $\varphi (0) = 0$ , which implies $K^\varphi _0(z) = 1$ for all $z \in \mathbb {D}$ .

It is well known that if a reproducing kernel function $K_w(z)=K(z,w)$ on $\mathbb {D}$ satisfies $K(z,0)=1$ for all $z\in \mathbb {D}$ , then it is a CNP kernel if and only if

$$ \begin{align*}1-\frac1{K(z,w)}\succeq 0.\end{align*} $$

See [3, p. 88] for example. Since

$$ \begin{align*}1 - \frac{1}{K^\varphi_w(z)} = 1 - \frac{(1-z\overline{w})^2}{1-\varphi(z)\overline{\varphi(w)}} = \frac{2z\overline{w}-z^2\overline{w^2}-\varphi(z)\overline{\varphi(w)}}{1-\varphi(z)\overline{\varphi(w)}},\end{align*} $$

we have

$$ \begin{align*}\frac{1-\frac{z}{\sqrt{2}}\frac{\overline{w}}{\sqrt{2}}-\frac{\varphi(z)}{\sqrt{2}z}\frac{\overline{\varphi(w)}}{\sqrt{2}\overline{w}}}{1-\varphi(z)\overline{\varphi(w)}} \succeq 0.\end{align*} $$

It follows from this and Lemma 3.1 that

(3.2) $$ \begin{align} \Phi(z) = \left(\frac{z}{\sqrt{2}}, \frac{\varphi(z)}{\sqrt{2}z}\right) \in \mathcal{M}_1\Bigl(H(K^{H^2}\circ \varphi) \otimes \mathbb{C}^2, H(K^{H^2}\circ \varphi)\Bigr). \end{align} $$

Thus,

$$ \begin{align*}\frac{z}{\sqrt{2}}\in \mathcal{M}_1(H(K^{H^2}\circ \varphi)),\quad \frac{\varphi(z)}{\sqrt{2}z} \in \mathcal{M}_1(H(K^{H^2}\circ \varphi)).\end{align*} $$

Using $z/\sqrt {2} \in \mathcal {M}_1(H(K^{H^2}\circ \varphi ))$ and $1 \in H(K^{H^2}\circ \varphi )$ , we can find a function $h \in H^2$ such that

(3.3) $$ \begin{align} \frac{z}{\sqrt{2}} = \frac{z}{\sqrt{2}} (1) = h(\varphi(z)),\quad z \in \mathbb{D}. \end{align} $$

Therefore, $\varphi $ is injective, and by Lemma 3.2, $h \in \mathcal {M}_1(H^2) = H^\infty _1$ and $h(0) = 0$ . Similarly, we deduce from $\varphi (z)/(\sqrt {2}\,z) \in \mathcal {M}_1(H(K^{H^2}\circ \varphi ))$ that $z/(2h) \in H^\infty _1$ . Then (3.2) implies that

$$ \begin{align*}T: = \left(h, \frac{z}{2h}\right) \in \text{Mult}_1(H^2 \otimes \mathbb{C}^2, H^2).\end{align*} $$

Since

$$ \begin{align*}T^* \frac{1}{1-\overline{\lambda}z} = \left(\overline{h(\lambda)}, \overline{\frac{z}{2h}(\lambda)}\,\right) \frac{1}{1-\overline{\lambda}z},\end{align*} $$

we conclude that

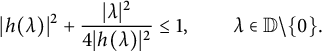$$ \begin{align*}|h(\lambda)|^2 + \frac{|\lambda|^2}{4|h(\lambda)|^2} \leq 1, \qquad\lambda \in \mathbb{D}\setminus\{0\}.\end{align*} $$

Passing to boundary limits, we obtain

$$ \begin{align*}|h(\lambda)|^2 + \frac{1}{4|h(\lambda)|^2} \leq 1\end{align*} $$

for almost all $\lambda \in \mathbb {T}$ . It follows that $|h(\lambda )| = \frac {1}{\sqrt {2}}$ for almost all $\lambda \in \mathbb {T}$ . Thus, $\sqrt {2}h$ is an inner function. By the Schwarz lemma, the inequality $\sqrt 2|h(z)|\le 1$ together with $h(0)=0$ implies that $\sqrt 2|h(z)|\le |z|$ on $\mathbb {D}$ . This along with $z/(2h)\in H^\infty _1$ shows that

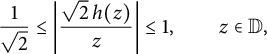$$ \begin{align*}\frac1{\sqrt2}\le\left|\frac{\sqrt2\,h(z)}{z}\right|\le1,\qquad z\in\mathbb{D},\end{align*} $$

which implies that the inner function $\sqrt 2 h(z)/z$ has no zero inside $\mathbb {D}$ and has no singular factor. Therefore, $\sqrt {2}h(z) = \zeta z$ for some $\zeta \in \mathbb {T}$ . It then follows from (3.3) that $\varphi (z) = \overline {\zeta }z$ , which finishes the proof of the theorem.

The characterization of CNP kernels for the sub- $A^2_\alpha $ spaces $H^\alpha (\varphi )$ are more subtle though. The results we obtain will depend on the range of the parameter $\alpha $ .

Theorem 3.4 Suppose $\varphi \in H^\infty _1$ and $-1<\alpha \le 0$ . Then the reproducing kernel of $H^\alpha (\varphi )$ in (2.3) is a CNP kernel if and only if $\varphi $ is a Möbius map.

Proof The case $\alpha =0$ concerns the ordinary Bergman space, which is Theorem 3.3. So we assume $-1<\alpha <0$ for the rest of this proof.

First, assume that $\varphi $ is a Möbius map, say $\varphi (z)=\zeta \,\frac {a-z}{1-\overline az}$ with $\zeta \in \mathbb {T}$ and $a\in \mathbb {D}$ . Then an easy computation shows that the reproducing kernel for $H^\alpha (\varphi )$ can be written as

$$ \begin{align*}K(z,w)=\frac{1-|a|^2}{(1-\overline az)(1-a\overline w)}\,\frac1{(1-z\overline w)^{1+\alpha}},\end{align*} $$

which is known to be a CNP kernel. See [3].

Next, we assume that the kernel for $H^\alpha (\varphi )$ in (2.3) is a CNP kernel. Once again, by considering $\psi (z)=\varphi _a\circ \varphi (z)$ with $a=\varphi (0)$ and using (3.1), we may assume that $\varphi (0)=0$ .

When $\varphi (0)=0$ , we have $K^{\alpha ,\varphi }_0(z)=1$ for all $z\in \mathbb {D}$ . In this case, it is known that the kernel $K^{\alpha ,\varphi }_w(z)$ is CNP if and only if $1-[1/K^{\alpha ,\varphi }_w(z)]\succeq 0$ (see [3] for example). Since

$$ \begin{align*} 1&-\frac1{K^{\alpha,\varphi}_w(z)}=1-\frac{(1-z\overline w)^{2+\alpha}}{1-\varphi(z)\overline{\varphi(w)}}\\ &=\left[sz\overline w-\sum_{n=2}^\infty\frac{s(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}\, z^n\overline w^n-\varphi(z)\overline{\varphi(w)}\,\right]\,\frac1{1-\varphi(z)\overline{\varphi(w)}}, \end{align*} $$

where $s=\alpha +2\in (1,2)$ , we must have

$$ \begin{align*}\left[1-\sum_{n=2}^\infty\frac{(s-1)\,\Gamma(n-s)}{n!\,\Gamma(2-s)}\,z^{n-1}\overline w^{n-1}- \frac{\varphi(z)}{\sqrt s z}\,\frac{\overline{\varphi(w)}}{\sqrt s\overline w}\right]\,\frac1{1-\varphi(z)\overline{\varphi(w)}} \succeq 0.\end{align*} $$

Let

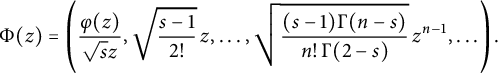$$ \begin{align*}\Phi(z)=\left(\frac{\varphi(z)}{\sqrt sz},\sqrt{\frac{s-1}{2!}}\,z,\ldots,\sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\, z^{n-1},\ldots\right).\end{align*} $$

By Lemma 3.1, we have

(3.4) $$ \begin{align} \Phi\in\mathcal{M}_1\Bigl(H(K^{H^2}\circ\varphi)\otimes l^2, H(K^{H^2}\circ\varphi)\Bigr). \end{align} $$

Thus,

$$ \begin{align*}\frac{\varphi(z)}{\sqrt sz},\quad\sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\,z^{n-1}\in \mathcal{M}_1\Bigl(H(K^{H^2}\circ\varphi)\Bigr),\qquad n\ge2.\end{align*} $$

It follows from

$$ \begin{align*}\sqrt{\frac{s-1}{2!}}\,z\in\mathcal{M}_1\Bigl(H(K^{H^2}\circ\varphi\Bigr),\quad 1\in H(K^{H^2}\circ\varphi),\end{align*} $$

that there exists some function $h\in H^2$ such that

(3.5) $$ \begin{align} \sqrt{\frac{s-1}{2}}\,z=\sqrt{\frac{s-1}{2}}\,h(\varphi(z)),\qquad z\in\mathbb{D}. \end{align} $$

Therefore, $\varphi $ is injective, and by Lemma 3.2,

$$ \begin{align*}\sqrt{\frac{s-1}{2}}\,h\in\mathcal{M}_1(H^2)=H^\infty_1\end{align*} $$

with $h(0)=0$ . Then we also have

$$ \begin{align*}\sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\,z^{n-1}= \sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\,h(\varphi(z))^{n-1},\qquad n\ge2.\end{align*} $$

Similarly, from $\varphi (z)/\sqrt sz\in \mathcal {M}_1(H(K^{H^2}\circ \varphi ))$ , we obtain $z/\sqrt sh\in H^\infty _1$ .

By (3.4), we must have

$$ \begin{align*} T(z)&:=\left(\frac z{\sqrt sh},\sqrt{\frac{s-1}{2!}}\,h,\ldots,\sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\,h^{n-1}, \ldots\right)\\ &\in\mathcal{M}_1(H^2\otimes l^2, H^2). \end{align*} $$

Note that

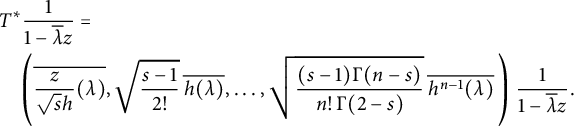$$ \begin{align*} &T^*\frac1{1-\overline\lambda z}=\\ &\quad\left(\overline{\frac z{\sqrt sh}(\lambda)},\sqrt{\frac{s-1}{2!}}\,\overline{h(\lambda)},\ldots, \sqrt{\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}}\,\overline{h^{n-1}(\lambda)}\,\right)\,\frac1{1-\overline\lambda z}. \end{align*} $$

It follows that

$$ \begin{align*}\frac{|\lambda|^2}{s|h(\lambda)|^2}+\sum_{n=2}^\infty\frac{(s-1)\Gamma(n-2)}{n!\,\Gamma(2-s)} \,|h(\lambda)|^{2n-2}\le1,\qquad\lambda\in\mathbb{D}\setminus\{0\}.\end{align*} $$

Passing to radial limits, we obtain

$$ \begin{align*}\frac1{s|h(\lambda)|^2}+\sum_{n=2}^\infty\frac{(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}\,|h(\lambda)|^{2n-2}\le1\end{align*} $$

or

$$ \begin{align*}1+\sum_{n=2}^\infty\frac{s(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}\,|h(\lambda)|^{2n}\le s|h(\lambda)|^2\end{align*} $$

for almost all $\lambda \in \mathbb {T}$ . We necessarily have $|h(\lambda )|^2\le 1$ . Comparing the above inequality with the classical Taylor series

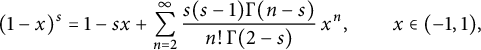$$ \begin{align*}(1-x)^s=1-sx+\sum_{n=2}^\infty\frac{s(s-1)\Gamma(n-s)}{n!\,\Gamma(2-s)}\,x^n,\qquad x\in(-1,1),\end{align*} $$

we obtain $(1-|h(\lambda )|^2)^s\le 0$ for almost all $\lambda \in \mathbb {T}$ , so h is an inner function. This together with $z/\sqrt sh\in H^\infty _1$ implies that $h(z)=\zeta z$ for some constant $\zeta \in \mathbb {T}$ . By (3.5), we have $\varphi (z)=\overline \zeta \,z$ . This completes the proof of the theorem.

Note that, in the case when $\alpha =-1$ , a characterization for $\varphi \in H^\infty _1$ was obtained in [10] in order for the kernel

$$ \begin{align*}K(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{(1-z\overline w)^{2+\alpha}}= \frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline w}\end{align*} $$

to be CNP. The necessary and sufficient condition for $\varphi $ is the following: there exists a function $h\in H^\infty _1$ such that $\psi (z)=zh(\psi (z))$ , where $\psi (z)=\varphi _a(\varphi (z))$ with $a=\varphi (0)$ .

When $-2<\alpha <-1$ , we have the following result.

Theorem 3.5 Suppose $-2<\alpha <-1$ and $\varphi \in \mathcal {M}_1(A^2_\alpha )$ . Let $a=\varphi (0)$ and $\psi =\varphi _a\circ \varphi $ . Then the function

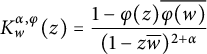$$ \begin{align*}K^{\alpha,\varphi}_w(z)=\frac{1-\varphi(z)\overline{\varphi(w)}}{(1-z\overline w)^{2+\alpha}}\end{align*} $$

is a CNP kernel if and only if there exists

$$ \begin{align*}h=(h_1, h_2,\ldots,h_n,\ldots)\in\mathcal{M}_1(H^2, H^2\otimes l^2)\end{align*} $$

such that

$$ \begin{align*}\psi(z)=\sum_{n=1}^\infty\sqrt{\frac{(2+\alpha)\Gamma(n-\alpha-2)}{n!\,\Gamma(-1-\alpha)}}\,z^nh_n(\psi(z))\end{align*} $$

on $\mathbb {D}$ .

Proof Recall from (3.1) that $K^{\alpha ,\varphi }_w(z)$ is a CNP kernel if and only if $K^{\alpha ,\psi }_w(z)$ is a CNP kernel. So we will assume that $\varphi (0)=0$ . In this case, we have $K^{\alpha ,\varphi }_0(z)=1$ for all $z\in \mathbb {D}$ and $1-[1/K^{\alpha ,\varphi }_w(z)]\succeq 0$ .

Let $s=\alpha +2$ and write

$$ \begin{align*} 1-\frac1{K^{\alpha,\varphi}_w(z)}&=1-\frac{(1-z\overline w)^s}{1-\varphi(z)\overline{\varphi(w)}}\\ &=\left(\sum_{n=1}^\infty\frac{s\Gamma(n-s)}{n!\,\Gamma(1-s)}\,z^n\overline w^n-\varphi(z)\overline{\varphi(w)}\right) \,\frac1{1-\varphi(z)\overline{\varphi(w)}}. \end{align*} $$

Since $1/(1-\varphi (z)\overline {\varphi (w)})$ is a CNP kernel, it follows from Theorem 8.57 of [3] that $1-[1/K^{\alpha ,\varphi }_w(z)]\succeq 0$ if and only if there exists

$$ \begin{align*}\Phi=(\varphi_n)\in\mathcal{M}_1\Bigl(H(K^{H^2}\circ\varphi), H(K^{H^2}\circ\varphi)\otimes l^2\Bigr)\end{align*} $$

such that

$$ \begin{align*}\varphi(z)=\sum_{n=1}^\infty\sqrt{\frac{s\Gamma(n-s)}{n!\,\Gamma(1-s)}}\,z^n\varphi_n(z).\end{align*} $$

By Lemma 3.2, there exist $h=(h_n)\subset H^\infty _1$ such that $\varphi _n(z)=h_n(\varphi (z))$ for all n and $h\in \text {Mult}_1(H^2, H^2\otimes l^2)$ . This proves the desired result.

For an example of a CNP kernel $K^{\alpha ,\varphi }_w(z)$ when $-2<\alpha <-1$ , fix any positive integer n and consider

$$ \begin{align*}\varphi(z)=\sqrt{\frac{(2+\alpha)\Gamma(n-2-\alpha)}{n!\,\Gamma(-1-\alpha)}}\,z^n.\end{align*} $$

It is easy to see that $\varphi \in \mathcal {M}_1(A^2_\alpha )$ and, by the theorem above, $K^{\alpha ,\varphi }_w(z)$ is a CNP kernel. Also, if $h = (\frac {1}{2}, \frac {1}{4}, \ldots , \frac {1}{2^n}, \ldots )$ , and

$$ \begin{align*}\varphi(z) = \sum_{n=1}^\infty\sqrt{\frac{(2+\alpha)\Gamma(n-2-\alpha)}{n!\,\Gamma(-1-\alpha)}}\,\frac{z^n}{2^n},\end{align*} $$

then $h \in \text {Mult}_1(H^2, H^2\otimes l^2)$ , $\varphi \in \mathcal {M}_1(A^2_\alpha )$ , and $K^{\alpha ,\varphi }_w(z)$ is a CNP kernel.

When $\alpha>0$ , the identity function $\varphi (z)=z$ belongs to $H^\infty _1= \mathcal {M}_1(A^2_\alpha )$ , but

$$ \begin{align*}K^{\alpha,\varphi}_w(z)=\frac{1-z\overline w}{(1-z\overline w)^{2+\alpha}}=\frac1{(1-z\overline w)^{1+\alpha}}\end{align*} $$

is NOT a CNP kernel (see [3]). In fact, when $\alpha> 0$ , $K^{\alpha ,\varphi }_w(z)$ is not a CNP kernel for any $\varphi \in \mathcal {M}_1(A^2_\alpha ) = H^\infty _1$ . The following result was communicated to us by Michael Hartz.

Theorem 3.6 [16]

Suppose $\alpha> 0$ and $\varphi \in H^\infty _1$ . Then $K^{\alpha ,\varphi }_w(z)$ is not a CNP kernel.

Proof We prove it by contradiction. Suppose $K^{\alpha ,\varphi }_w(z)$ is a CNP kernel. By the same observation as before, we may assume $\varphi (0) = 0$ . Note that when $\alpha> 0$ ,

$$ \begin{align*}\frac{1-\varphi(z)\overline{\varphi(w)}}{(1-z\overline{w})^{1+\alpha}} \succeq 0.\end{align*} $$

Thus, let $S_w(z) = 1/(1-z\overline {w})$ be the Szegő kernel, then $K^{\alpha , \varphi }/S$ is positive-definite. Then an application of the Schur product theorem shows that $H^\infty (\mathbb {D}) = \mathcal {M}(H^2)$ is contractively contained in $\mathcal {M}(H^\alpha (\varphi ))$ (see [15, Corollary 3.5] or the proof in Lemma 4.2). Since $\mathcal {M}(H^\alpha (\varphi ))$ is also contractively contained in $H^\infty (\mathbb {D})$ , we conclude that $\mathcal {M}(H^\alpha (\varphi )) = H^\infty (\mathbb {D})$ with equality of norms.

Now, a normalized CNP kernel is uniquely determined by its multiplier algebra (see [15, Corollary 3.2]). Since $K^{\alpha , \varphi }_w(z)$ and $S_w(z)$ are CNP kernels, it follows that $K^{\alpha , \varphi }_w(z) = S_w(z)$ . Thus,

$$ \begin{align*}1-\varphi(z)\overline{\varphi(w)} = (1-z\overline{w})^{1+\alpha}, \quad z, w \in \mathbb{D}.\end{align*} $$

Setting $w =z$ , we obtain that

$$ \begin{align*}1-|\varphi(z)|^2 = (1 - |z|^2)^{1+\alpha}.\end{align*} $$

But by the Schwarz lemma, $|\varphi (z)| \leq |z|$ , from which we see that the above equation cannot be held when $\alpha> 0$ . This contraction then finishes the proof.

The above argument also works for $\alpha = 0$ , and it provides a different proof of Theorem 3.3.

4 Compactness of defect operators

In this section, we will characterize functions $\varphi \in H^\infty _1$ such that the defect operators $D^\alpha _\varphi $ and $D^\alpha _{\overline \varphi }$ , where $\alpha>-1$ , are compact. The following result follows from I-9 of [21].

Lemma 4.1 Let $\alpha> -1$ , $\varphi \in H^\infty _1$ , and $M^\alpha (\varphi ) = \varphi A^2_\alpha $ . Then

$$ \begin{align*}H^\alpha(\varphi) \cap M^\alpha(\varphi) = \varphi H^\alpha(\overline{\varphi}).\end{align*} $$

The following result was proved in [18, 23]. We provide a different proof here.

Lemma 4.2 Let $\alpha> -1$ and $\varphi \in H^\infty _1$ . If $\varphi $ is a finite Blaschke product, then

$$ \begin{align*}H^\alpha(\overline\varphi) = H^\alpha(\varphi) = A^2_{\alpha-1}.\end{align*} $$

Proof By the definition of $A^2_{\alpha -1}$ , it is not hard to see that any function that is analytic on the closed unit disk is a multiplier of $A^2_{\alpha -1}$ . In particular, $T_\varphi $ is a bounded operator on $A^2_{\alpha -1}$ . If $\|T_{\varphi }\|_{B(A^2_{\alpha -1})} = C < \infty $ , then

$$ \begin{align*}(I- T_{\varphi} T_{\varphi}^*/C^2)K^{\alpha-1}_w(z) = \frac{1-\varphi(z)\overline{\varphi(w)}/C^2}{(1-z\overline{w})^{1+\alpha}} \succeq 0.\end{align*} $$

Thus, by the Schur product theorem [19],

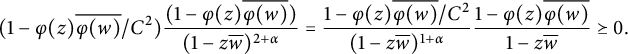$$ \begin{align*}(1-\varphi(z)\overline{\varphi(w)}/C^2)\frac{(1-\varphi(z)\overline{\varphi(w)})}{(1-z\overline{w})^{2+\alpha}} = \frac{1-\varphi(z)\overline{\varphi(w)}/C^2}{(1-z\overline{w})^{1+\alpha}}\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}} \succeq 0.\end{align*} $$

It follows that $\varphi /C$ is a contractive multiplier of $H^{\alpha }(\varphi )$ . Thus, $\varphi H^{\alpha }(\varphi ) \subseteq H^{\alpha }(\varphi )$ . Combining this with $H^{\alpha }(\varphi ) \subseteq A^2_\alpha $ , we obtain

$$ \begin{align*}\varphi H^{\alpha}(\varphi) \subseteq H^{\alpha}(\varphi) \cap \varphi A^2_\alpha = H^{\alpha}(\varphi) \cap M^\alpha(\varphi).\end{align*} $$

By Lemma 4.1, we then have $\varphi H^{\alpha }(\varphi ) \subseteq \varphi H^{\alpha }(\overline {\varphi })$ , so $H^{\alpha }(\varphi ) \subseteq H^{\alpha }(\overline {\varphi })$ .

To finish the proof, we note $H^{\alpha }(\varphi ) = A^2_{\alpha -1}$ [22] and use the fact that the subnormality of $T_\varphi $ gives $H^{\alpha }(\overline {\varphi }) \subseteq H^{\alpha }(\varphi )$ in general.

Lemma 4.3 Let $\varphi $ be a nonconstant function in $H^\infty _1$ . Then the following conditions are equivalent.

1. (a) $\varphi $ is a finite Blaschke product.

2. (b) $1-|\varphi (z)|^2\to 0$ as $|z|\to 1^-$ .

3. (c) $(1-|\varphi (z)|^2)/(1-|z|^2)$ is bounded both above and below on $\mathbb {D}$ .

Proof The equivalence of (a) and (c) was proved in [26]. It is trivial that (c) implies (b).

If (b) holds, then $|\varphi (z)|\to 1$ uniformly as $|z|\to 1^-$ , so $\varphi $ is an inner function. It is clear that $\varphi $ cannot have infinitely many zeros. If $\varphi $ contains a singular inner factor S, then there exists at least one point $\zeta \in \mathbb {T}$ such that $S(z)\to 0$ as z approaches $\zeta $ radially, which contradicts with the limit $|\varphi (z)|\to 1$ as $|z|\to 1^-$ . Thus, $\varphi $ cannot contain any singular inner factor. Hence, $\varphi $ must be a finite Blaschke product. This shows that (b) implies (a) and completes the proof of the lemma.

Lemma 4.4 Suppose $\alpha>-1$ and $T: A^2_\alpha \to A^2_\alpha $ is a bounded linear operator. If the range of T is contained in $A^2_\gamma $ for some $\gamma <\alpha $ , then T belongs to the Schatten class $S_p$ for all $p>2/(\alpha -\gamma )$ .

Proof It is well known that if $\gamma <\alpha $ , then $A^2_\gamma \subset A^2_\alpha $ , and the inclusion mapping $i: A^2_\gamma \to A^2_\alpha $ is bounded. If T maps $A^2_\alpha $ into $A^2_\gamma $ , then by the closed graph theorem, there exists a constant $C>0$ such that $\|Tf\|_{A^2_\gamma }\le C\|f\|_{A^2_\alpha }$ for all $f\in A^2_\alpha $ , that is, T can be thought of as a bounded linear operator from $A^2_\alpha $ into $A^2_\gamma $ . We can then write $T=iT$ and $T^*T=T^*(i^*i)T$ .

The operator $i^*i: A^2_\gamma \to A^2_\gamma $ is positive. With respect to the monomial orthonormal basis $\{e_n=c_nz^n\}$ of $A^2_\gamma $ from Section 2, the operator $i^*i$ is diagonal with the corresponding eigenvalues given by

$$ \begin{align*}\langle i^*ie_n, e_n\rangle_{A^2_\gamma}=c_n^2\langle z^n, z^n\rangle_{A^2_\alpha} =\frac{\Gamma(n+2+\gamma)}{n!\,\Gamma(2+\gamma)}\,\frac{n!\,\Gamma(2+\alpha)}{\Gamma(n+2+\alpha)} \sim\frac1{(n+1)^{\alpha-\gamma}},\end{align*} $$

as $n\to \infty $ . This shows that $i^*i$ belongs to the Schatten class $S_p$ of $A^2_\gamma $ for all p with $p(\alpha -\gamma )>1$ . Thus, T belongs to the Schatten class $S_p$ of $A^2_\alpha $ whenever $p>2/(\alpha -\gamma )$ .

Note that the result above remains true even if the parameters $\alpha $ and $\gamma $ fall below $-1$ , although the proof needs to be modified. Details are omitted. We now prove the main results of this section in the next two theorems.

Recall that

$$ \begin{align*}D_\varphi^\alpha = \left(I-T_\varphi T_\varphi^*\right)^{1/2},\qquad D_{\overline\varphi}^\alpha=\left(I-T_\varphi^*T_\varphi\right)^{1/2}\end{align*} $$

are the defect operators, and

$$ \begin{align*}E_\varphi^\alpha=I-T_\varphi T_\varphi^*,\qquad E_{\overline\varphi}^\alpha=I-T_\varphi^*T_\varphi.\end{align*} $$

Theorem 4.5 Suppose $\alpha>-1$ and $\varphi \in H^\infty _1$ . Then the following conditions are equivalent.

1. (a) The defect operator $D^\alpha _\varphi $ is compact on $A^2_\alpha $ .

2. (b) The function $\varphi $ is a finite Blaschke product.

3. (c) The space $H^\alpha (\varphi )$ equals $A^2_{\alpha -1}$ .

4. (d) The space $H^\alpha (\varphi )$ is contained in $A^2_{\alpha -1}$ .

Proof To prove (a) implies (b), we consider the normalized reproducing kernels

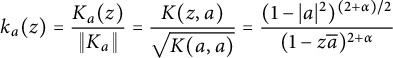$$ \begin{align*}k_a(z)=\frac{K_a(z)}{\|K_a\|}=\frac{K(z,a)}{\sqrt{K(a,a)}}=\frac{(1-|a|^2)^{(2+\alpha)/2}}{(1-z\overline a)^{2+\alpha}}\end{align*} $$

for $A^2_\alpha $ . It is easy to see that $k_a\to 0$ weakly in $A^2_\alpha $ as $|a|\to 1^-$ . If $D^\alpha _\varphi $ is compact, then so is $E^\alpha _\varphi $ , which implies that $\langle E^\alpha _\varphi k_a, k_a\rangle \to 0$ as $|a|\to 1^-$ . It is easy to see that $T^*_\varphi k_a=\overline {\varphi (a)}\,k_a$ , so we have

$$ \begin{align*} \langle E^\alpha_\varphi k_a, k_a\rangle=\langle(I-T_\varphi T^*_\varphi)k_a, k_a\rangle =1-\langle T^*_\varphi k_a, T^*_\varphi k_z\rangle=1-|\varphi(a)|^2. \end{align*} $$

Thus, the compactness of $D^\alpha _\varphi $ implies $1-|\varphi (a)|^2\to 0$ as $|a|\to 1^-$ , which, according to Lemma 4.3, shows that $\varphi $ is a finite Blaschke product. This proves (a) implies (b).

Lemma 4.2 states that (b) implies (c). It is trivial that (c) implies (d). It follows from Lemma 4.4 that (d) implies (a). This completes the proof of the theorem.

Theorem 4.6 Suppose $\alpha>-1$ and $\varphi \in H^\infty _1$ . Then the following conditions are equivalent.

1. (a) The defect operator $D^\alpha _{\overline \varphi }$ is compact on $A^2_\alpha $ .

2. (b) The function $\varphi $ is a finite Blaschke product.

3. (c) The space $H^\alpha (\overline \varphi )$ equals $A^2_{\alpha -1}$ .

4. (d) The space $H^\alpha (\overline \varphi )$ is contained in $A^2_{\alpha -1}$ .

Proof First, assume that condition (a) holds. Taking the square of $D^\alpha _{\overline \varphi }$ , we see that the Toeplitz operator $T_{1-|\varphi |^2}$ (with nonnegative symbol) is compact on $A^2_\alpha $ . It follows from Corollary 7.9 of [27] that for any positive $r>0$ , we have

$$ \begin{align*}\lim_{|a|\to1^-}\frac1{A_\alpha(D(a,r))}\int_{D(a,r)}(1-|\varphi(z)|^2)\,dA_\alpha(z)=0,\end{align*} $$

where $D(a,r)=\{z\in \mathbb {D}: \beta (z,a)<r\}$ is the Bergman metric ball with center a and radius r, and $A_\alpha (D(a,r))$ is the $dA_\alpha $ measure of $D(a,r)$ . Equivalently,

(4.1) $$ \begin{align} \lim_{|a|\to1^-}\frac1{A_\alpha(D(a,r))}\int_{D(a,r)}|\varphi(z)|^2\,dA_\alpha(z)=1. \end{align} $$

We claim that this implies $|\varphi (z)|^2\to 1$ uniformly as $|z|\to 1^-$ . In fact, if this conclusion is not true, then there exist a constant $\sigma \in (0,1)$ and a sequence $\{a_n\}$ in $\mathbb {D}$ such that $|a_n|\to 1$ as $n\to \infty $ and $|\varphi (a_n)|<\sigma $ for all $n\ge 1$ .

If $z\in D(a_n, r)$ , then by Theorem 5.5 of [27],

$$ \begin{align*}|\varphi(z)|\le|\varphi(z)-\varphi(a_n)|+|\varphi(a_n)| \le\|\varphi\|_{\mathcal{B}}\,\beta(z,a_n)+\sigma<\|\varphi\|_{\mathcal{B}}r+\sigma,\end{align*} $$

where

$$ \begin{align*}\|\varphi\|_{\mathcal{B}}=\sup_{z\in\mathbb{D}}(1-|z|^2)|\varphi'(z)|\end{align*} $$

is Bloch seminorm of $\varphi $ (recall that every function in $H^\infty $ belongs to the Bloch space). If we use a sufficiently small radius r such that the constant $\delta =\|\varphi \|_{\mathcal {B}}r+\sigma <1$ , then

$$ \begin{align*}\frac1{A_\alpha(D(a_n,r))}\int_{D(a_n,r)}|\varphi(z)|^2\,dA_\alpha(z)\le\delta^2<1\end{align*} $$

for all $n\ge 1$ . This is a contradiction to (4.1).

Thus, we must have $|\varphi (z)|^2\to 1$ uniformly as $|z|\to 1^-$ . By Lemma 4.3, $\varphi $ is a finite Blaschke product. This proves that (a) implies (b).

It follows from Lemma 4.2 that (b) implies (c). It is trivial that (c) implies (d). That (d) implies (a) follows from Lemma 4.4.

It follows from the proof of the theorem above that, for $\alpha>-1$ , $k>0$ , and $\varphi \in H^\infty _1$ , the Toeplitz operator $T_{(1-|\varphi |^2)^k}$ is compact on $A^2_\alpha $ if and only if $\varphi $ is a finite Blaschke product.

5 The range of $I-T_\varphi T_{\varphi }^*$ and $I-T_{\varphi }^*T_\varphi $

In this section, we study the range of the operators $E^\alpha _\varphi $ and $E^\alpha _{\overline \varphi }$ . The special case $\alpha =0$ was considered in [26]. It is clear that $D^\alpha _\varphi $ is compact on $A^2_\alpha $ if and only if $E^\alpha _\varphi $ is compact on $A^2_\alpha $ . Similarly, $D^\alpha _{\overline \varphi }$ is compact on $A^2_\alpha $ if and only if $E^\alpha _{\overline \varphi }$ is compact on $A^2_\alpha $ .

Proposition 5.1 Suppose $\alpha>-1$ and $\varphi $ is a finite Blaschke product. Then

(5.1) $$ \begin{align} A^2_{\alpha-1}&=\left\{f(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,g(w)\,dA_\alpha(w): g\in A^2_{\alpha+1}\right\} \end{align} $$

(5.2) $$ \begin{align} &=\left\{f(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,g(w)\,dA_\alpha(w): g\in L^2(\mathbb{D}, dA_{\alpha+1})\right\}. \end{align} $$

Proof Let

$$ \begin{align*}dA_{\varphi,\alpha}(z)=(1-|\varphi(z)|^2)\,dA_\alpha(z),\end{align*} $$

and let $A^2_{\varphi ,\alpha }$ denote the space of analytic functions in $L^2(\mathbb {D}, dA_{\varphi ,\alpha })$ . It follows from Lemma 4.3 that

$$ \begin{align*}L^2(\mathbb{D}, dA_{\varphi,\alpha})=L^2(\mathbb{D}, dA_{\alpha+1}),\qquad A^2_{\varphi,\alpha} =A^2_{\alpha+1},\end{align*} $$

with equivalent norms. Consider the integral operator $S_\varphi : A^2_{\varphi ,\alpha }\to A^2_\alpha $ defined by

(5.3) $$ \begin{align} S_\varphi f(z)=P_\alpha[(1-|\varphi|^2)f](z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,f(w)\,dA_\alpha(w), \end{align} $$

where $P_\alpha : L^2(\mathbb {D}, dA_\alpha )\to A^2_\alpha $ is the orthogonal projection. It is clear that $S_\varphi $ is simply the operator $E^\alpha _{\overline \varphi }$ with its domain extended to the larger space $A^2_{\varphi ,\alpha }$ .

Now, the first desired equality (5.1) follows from the proof of Proposition 3.5 in [25], word by word, together with the fact that $H^\alpha (\overline \varphi )=A^2_{\alpha -1}$ from the previous section. The second equality (5.2) follows from the same argument by replacing the operator $S_\varphi $ above by its extension $S_\varphi : L^2(\mathbb {D}, dA_{\varphi ,\alpha })\to A^2_\alpha $ , still defined by (5.3). We leave the details to the interested reader but summarize the main points of this omitted argument as follows.

For both

$$ \begin{align*}S_\varphi: A^2_{\varphi,\alpha}\to A^2_\alpha\quad\mathrm{and}\quad S_\varphi: L^2(\mathbb{D}, dA_{\varphi,\alpha})\to A^2_\alpha,\end{align*} $$

the adjoint $S_\varphi ^*$ is simply the inclusion, the image H of $S_\varphi $ is a reproducing kernel Hilbert space with the inner product

$$ \begin{align*}\langle S_\varphi f, S_\varphi g\rangle_H=\langle f,g \rangle_{L^2(\mathbb{D},dA_{\varphi,\alpha})},\qquad f,g\in\ker(S_\varphi)^\perp,\end{align*} $$

and the reproducing kernel of H at w is $S_\varphi S_\varphi ^*K_w ^\alpha $ , where $K^\alpha _w$ is the reproducing kernel of $A^2_\alpha $ at w. Consequently, the reproducing kernel of H is given by

$$ \begin{align*}S_\varphi K_w^\alpha(z)=\int_{\mathbb{D}}\frac{1-|\varphi(u)|^2}{(1-z\overline u)^{2+\alpha} (1-u\overline w)^{2+\alpha}}\,dA_\alpha(u),\end{align*} $$

which coincides with the reproducing kernel of $H^\alpha (\overline \varphi )$ . By uniqueness of the reproducing kernel, we must have $H=H^\alpha (\overline \varphi ) =A^2_{\alpha -1}$ , which yields the desired representations in (5.1) and (5.2).

Lemma 5.2 If $\alpha>-1$ and $\varphi $ is a finite Blaschke product, then

$$ \begin{align*}E^\alpha_\varphi(A^2_\alpha)=E^\alpha_{\overline\varphi}(A^2_\alpha)=A^2_{\alpha-2}.\end{align*} $$

Proof As a Toeplitz operator on $A^2_\alpha $ , we can write

$$ \begin{align*}E^\alpha_{\overline\varphi}f(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,f(w)\,dA_\alpha(w), \qquad f\in A^2_\alpha.\end{align*} $$

It follows that

$$ \begin{align*}(E^\alpha_{\overline\varphi}f)'(z)=\int_{\mathbb{D}}\frac{\Phi(w)}{(1-z\overline w)^{3+\alpha}}\,f(w)\,dA_{\alpha+1}(w) =P_{\alpha+1}(\Phi f)(z),\end{align*} $$

where $P_{\alpha +1}: L^2(\mathbb {D}, dA_{\alpha +1})\to A^2_{\alpha +1}$ is the orthogonal projection and

$$ \begin{align*}\Phi(w)=\frac{(\alpha+1)\overline w(1-|\varphi(w)|^2)}{1-|w|^2}.\end{align*} $$

By Lemma 4.3, $\Phi \in L^\infty (\mathbb {D})$ . It follows from Theorem 3.11 of [27] that $P_{\alpha +1}$ maps $L^2(\mathbb {D}, dA_\alpha )$ boundedly to $A^2_\alpha $ . Therefore, $f\in A^2_\alpha $ implies $(E^\alpha _{\overline \varphi }f)'\in A^2_{\alpha }$ , which is clearly equivalent to $E^\alpha _{\overline \varphi }f \in A^2_{\alpha -2}$ . This proves that $E^\alpha _{\overline \varphi }$ maps $A^2_\alpha $ into $A^2_{\alpha -2}$ .

To show that the mapping $E^\alpha _{\overline \varphi }: A^2_\alpha \to A^2_{\alpha -2}$ is onto, we switch from the ordinary derivative $(E^\alpha _{\overline \varphi }f)'$ to a certain fractional radial differential operator R ( $=R^{2+\alpha ,1}$ using the notation from [24]) of order $1$ :

$$ \begin{align*}RE^\alpha_{\overline\varphi}f(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{3+\alpha}}\,f(w)\,dA_\alpha(w).\end{align*} $$

It is still true that $E^\alpha _{\overline \varphi }f\in A^2_{\alpha -2}$ if and only if $RE^\alpha _{\overline \varphi }f\in A^2_\alpha $ . See [24].

Fix any function $g\in A^2_{\alpha -2}$ . Then the function $Rg$ belongs to $A^2_\alpha $ . It follows from Proposition 5.1, with $\alpha $ in (5.1) and (5.2) replaced by $\alpha +1$ , that there exists a function $h\in L^2(\mathbb {D}, dA_{\alpha +2})$ such that

$$ \begin{align*}Rg(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{3+\alpha}}\,h(w)\,dA_{\alpha+1}(w).\end{align*} $$

Applying the inverse of R to both sides, we obtain

$$ \begin{align*}g(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,h(w)\,dA_{\alpha+1}(w).\end{align*} $$

Let $\widetilde h(w)=(1-|w|^2)h(w)$ . Then $\widetilde h\in L^2(\mathbb {D}, dA_\alpha )$ and

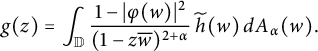$$ \begin{align*}g(z)=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,\widetilde h(w)\,dA_\alpha(w).\end{align*} $$

By Proposition 5.1 again, there exists a function $f\in A^2_\alpha $ such that

$$ \begin{align*}g=\int_{\mathbb{D}}\frac{1-|\varphi(w)|^2}{(1-z\overline w)^{2+\alpha}}\,f(w)\,dA_\alpha(w),\end{align*} $$

or $g=E^\alpha _{\overline \varphi }f$ . Thus, we have shown that $E^\alpha _{\overline \varphi }(A^2_\alpha ) =A^2_{\alpha -2}$ .

Next, we show that $E^\alpha _\varphi (A^2_\alpha )=A^2_{\alpha -2}$ . Note that $T_\varphi $ is a Fredholm operator. So $\varphi A^2_\alpha $ is closed in $A^2_\alpha $ , $\ker (T_\varphi ^*) = A^2_\alpha \ominus \varphi A^2_\alpha $ , and $A^2_\alpha = (A^2_\alpha \ominus \varphi A^2_\alpha )\oplus \varphi A^2_\alpha $ . Since

$$ \begin{align*}(I-T_\varphi T_\varphi^*)\varphi f =\varphi (I-T_\varphi^*T_\varphi) f, \quad f \in A^2_\alpha,\end{align*} $$

it follows that

$$ \begin{align*}E^\alpha_\varphi(A^2_\alpha)=(A^2_\alpha\ominus\varphi A^2_\alpha)\oplus \varphi E^\alpha_{\overline\varphi}(A^2_\alpha) = (A^2_\alpha\ominus\varphi A^2_\alpha)\oplus \varphi A^2_{\alpha-2}.\end{align*} $$

Since $A^2_\alpha \ominus \varphi A^2_\alpha $ consists of the reproducing kernels or the derivative of the reproducing kernels in $A^2_\alpha $ , we have $A^2_\alpha \ominus \varphi A^2_\alpha \subseteq A^2_{\alpha -2}$ . Also,

$$ \begin{align*}\dim (A^2_\alpha \ominus\varphi A^2_\alpha) = \dim (A^2_{\alpha-2} \ominus\varphi A^2_{\alpha-2}).\end{align*} $$

Thus, we obtain that

$$ \begin{align*}E^\alpha_\varphi(A^2_\alpha) = (A^2_{\alpha-2} \ominus\varphi A^2_{\alpha-2}) + \varphi A^2_{\alpha-2} = A^2_{\alpha-2},\end{align*} $$

completing the proof of the lemma.

We can now prove the main result of this section, namely, the next two theorems.

Theorem 5.3 Suppose $\alpha>-1$ and $\varphi \in H^\infty _1$ . Then the following conditions are equivalent.

1. (a) The operator $E^\alpha _{\varphi }$ is compact on $A^2_\alpha $ .

2. (b) The function $\varphi $ is a finite Blaschke product.

3. (c) The range of $E^\alpha _\varphi $ equals $A^2_{\alpha -2}$ .

4. (d) The range of $E^\alpha _\varphi $ is contained in $A^2_{\alpha -2}$ .

Proof Since $E^\alpha _\varphi =(D^\alpha _\varphi )^2$ , the operator $E^\alpha _\varphi $ is compact if and only if $D^\alpha _\varphi $ is compact. Thus, the equivalence of (a) and (b) follows from Theorem 4.5.

Lemma 5.2 shows that (b) implies (c). It is trivial that (c) implies (d). Finally, that (d) implies (a) follows from Lemma 4.4.

Theorem 5.4 Suppose $\alpha>-1$ and $\varphi \in H^\infty _1$ . Then the following conditions are equivalent.

1. (a) The operator $E^\alpha _{\overline \varphi }$ is compact on $A^2_\alpha $ .

2. (b) The function $\varphi $ is a finite Blaschke product.

3. (c) The range of $E^\alpha _{\overline \varphi }$ equals $A^2_{\alpha -2}$ .

4. (d) The range of $E^\alpha _{\overline \varphi }$ is contained in $A^2_{\alpha -2}$ .

Proof It is similar to the proof of Theorem 5.3.

Finally, we note that the main results of this and the previous section cannot be extended to the Hardy space $H^2$ (the case $\alpha =-1$ ). For example, in this case, if $\varphi (z)=z$ , then $I-T_{\overline \varphi }T_{\varphi }=0$ and $I-T_\varphi T_{\overline \varphi }$ is a rank-one operator. More generally, if $\varphi $ is any inner function, then $I-T_{\overline \varphi }T_\varphi =0$ .