We prove that a Hamiltonian $p\in {{C}^{\infty }}({{T}^{*}}{{\mathbf{R}}^{n}})$ is locally integrable near a non-degenerate critical point ${{\rho }_{0}}$ of the energy, provided that the fundamental matrix at ${{\rho }_{0}}$ has rationally independent eigenvalues, none purely imaginary. This is done by using Birkhoff normal forms, which turn out to be convergent in the ${{C}^{\infty }}$ sense. We also give versions of the Lewis-Sternberg normal form near a hyperbolic fixed point of a canonical transformation. Then we investigate the complex case, showing that when $p$ is holomorphic near ${{\rho }_{0}}\in {{T}^{*}}{{\mathbf{C}}^{n}},$ then Re $p$ becomes integrable in the complex domain for real times, while the Birkhoff series and the Birkhoff transforms may not converge, i.e.,$p$ may not be integrable. These normal forms also hold in the semi-classical frame.

We study the Riemannian Laplace-Beltrami operator $L$ on a Riemannian manifold with Heisenberg group ${{H}_{1}}$ as boundary. We calculate the heat kernel and Green's function for $L$, and give global and small time estimates of the heat kernel. A class of hypersurfaces in this manifold can be regarded as approximations of ${{H}_{1}}$. We also restrict $L$ to each hypersurface and calculate the corresponding heat kernel and Green's function. We will see that the heat kernel and Green's function converge to the heat kernel and Green's function on the boundary.

We examine the problem of finding rational points defined over solvable extensions on algebraic curves defined over general fields. We construct non-singular, geometrically irreducible projective curves without solvable points of genus $g$, when $g$ is at least 40, over fields of arbitrary characteristic. We prove that every smooth, geometrically irreducible projective curve of genus 0, 2, 3 or 4 defined over any field has a solvable point. Finally we prove that every genus 1 curve defined over a local field of characteristic zero with residue field of characteristic $p$ has a divisor of degree prime to $6p$ defined over a solvable extension.

Let $G=\text{S}{{\text{p}}_{\text{2n}}}$ be the symplectic group defined over a number field $F$. Let $\mathbb{A}$ be the ring of adeles. A fundamental problem in the theory of automorphic forms is to decompose the right regular representation of $G\left( \mathbb{A} \right)$ acting on the Hilbert space ${{L}^{2}}\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)$. Main contributions have been made by Langlands. He described, using his theory of Eisenstein series, an orthogonal decomposition of this space of the form: $L_{dis}^{2}\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)\,=\,{{\oplus }_{\left( M,\,\pi \right)}}L_{dis}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\,\pi \right)}},\,\text{where}\,\left( M,\,\pi \right)$ is a Levi subgroup with a cuspidal automorphic representation $\pi $ taken modulo conjugacy. (Here we normalize $\pi $ so that the action of the maximal split torus in the center of $G$ at the archimedean places is trivial.) and $L_{\text{dis}}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\pi \right)}}$ is a space of residues of Eisenstein series associated to $\left( M,\,\pi \right)$. In this paper, we will completely determine the space $L_{\text{dis}}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\pi \right)}}$, when $M\simeq \text{G}{{\text{L}}_{2}}\times \text{G}{{\text{L}}_{2}}$. This is the first result on the residual spectrum for non-maximal, non-Borel parabolic subgroups, other than $\text{G}{{\text{L}}_{n}}$.

It is well known that multiple polylogarithms give rise to good unipotent variations of mixed Hodge-Tate structures. In this paper we shall explicitly determine these structures related to multiple logarithms and some other multiple polylogarithms of lower weights. The purpose of this explicit construction is to give some important applications. First we study the limit of mixed Hodge-Tate structures and make a conjecture relating the variations of mixed Hodge-Tate structures of multiple logarithms to those of general multiple polylogarithms. Then following Deligne and Beilinson we describe an approach to defining the single-valued real analytic version of the multiple polylogarithms which generalizes the well-known result of Zagier on classical polylogarithms. In the process we find some interesting identities relating single-valued multiple polylogarithms of the same weight $K$ when $K=2$ and 3. At the end of this paper, motivated by Zagier's conjecture we pose a problem which relates the special values of multiple Dedekind zeta functions of a number field to the single-valued version of multiple polylogarithms.

In this paper we extend Darmon's theory of “integration on ${{\text{H}}_{p}}\times \text{H}$” to cusp forms $f$ of higher even weight. This enables us to prove a “weak exceptional zero conjecture”: that when the $p$-adic $L$-function of $f$ has an exceptional zero at the central point, the $\mathcal{L}$-invariant arising is independent of a twist by certain Dirichlet characters.

We study the type decomposition and the rectangular $\text{AFD}$ property for ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$. Like von Neumann algebras, every ${{W}^{*}}-\text{TRO}$ can be uniquely decomposed into the direct sum of ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of $\text{type}\,I,\,\text{type}\,II$, and $\text{type}\,III$. We may further consider ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of $\text{type}\,{{I}_{m,n}}$ with cardinal numbers $m$ and $n$, and consider ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of $type\,I{{I}_{\lambda ,\mu }}\,\text{with}\,\lambda ,\,\mu \,=\,1\,\text{or}\,\infty $. It is shown that every separable stable ${{W}^{*}}-\text{TRO}$ (which includes 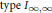$\text{type}\,{{I}_{\infty ,\infty }}$, $\text{type}\,I{{I}_{\infty ,\infty }}$ and $\text{type}\,III$) is $\text{TRO}$-isomorphic to a von Neumann algebra. We also introduce the rectangular version of the approximately finite dimensional property for ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$. One of our major results is to show that a separable ${{W}^{*}}-\text{TRO}$ is injective if and only if it is rectangularly approximately finite dimensional. As a consequence of this result, we show that a dual operator space is injective if and only if its operator predual is a rigid rectangular $\mathcal{O}{{\mathcal{L}}_{1,{{1}^{+}}}}$ space (equivalently, a rectangular $\mathcal{O}{{\mathcal{L}}_{1,{{1}^{+}}}}$ space).

We classify the generalized hexagons which are laxly embedded in projective space such that the embedding is flat and polarized. Besides the standard examples related to the hexagons defined over the algebraic groups of type ${{\text{G}}_{2}}$, ${}^{3}{{\text{D}}_{4}}$ and ${}^{6}{{\text{D}}_{\text{4}}}$ (and occurring in projective dimensions 5, 6, 7), we find new examples in unbounded dimension related to the mixed groups of type ${{\text{G}}_{2}}$ .

We consider symmetries of the Dedonder equation arising from variational problems with partial derivatives. Assuming a proper action of the symmetry group, we identify a set of reduced equations on an open dense subset of the domain of definition of the fields under consideration. By continuity, the Dedonder equation is satisfied whenever the reduced equations are satisfied.

This paper addresses the problem of constructing a cycle-level intersection theory for toric varieties. We show that by making one global choice, we can determine a cycle representative for the intersection of an equivariant Cartier divisor with an invariant cycle on a toric variety. For a toric variety defined by a fan in $N$, the choice consists of giving an inner product or a complete flag for ${{M}_{\mathbb{Q}}}\,=\,\mathbb{Q}\,\otimes \,\text{Hom(}N,\,\mathbb{Z}\text{)}$ , or more generally giving for each cone σ in the fan a linear subspace of ${{M}_{\mathbb{Q}}}$ complementary to ${{\sigma }^{\bot }}$ , satisfying certain compatibility conditions. We show that these intersection cycles have properties analogous to the usual intersections modulo rational equivalence. If $X$ is simplicial (for instance, if $X$ is non-singular), we obtain a commutative ring structure to the invariant cycles of $X$ with rational coefficients. This ring structure determines cycles representing certain characteristic classes of the toric variety. We also discuss how to define intersection cycles that require no choices, at the expense of increasing the size of the coefficient field.

We construct analogues of theta series, Eisenstein series and Poincaré series for function fields of one variable over finite fields, and prove their basic properties.

A coplactic class in the symmetric group ${{\mathcal{S}}_{n}}$ consists of all permutations in ${{\mathcal{S}}_{n}}$ with a given Schensted $Q$-symbol, and may be described in terms of local relations introduced by Knuth. Any Lie element in the group algebra of ${{\mathcal{S}}_{n}}$ which is constant on coplactic classes is already constant on descent classes. As a consequence, the intersection of the Lie convolution algebra introduced by Patras and Reutenauer and the coplactic algebra introduced by Poirier and Reutenauer is the direct sum of all Solomon descent algebras.

Suppose $K$ is an imaginary quadratic field and $E$ is an elliptic curve over a number field $F$ with complex multiplication by the ring of integers in $K$. Let $p$ be a rational prime that splits as ${{\mathfrak{p}}_{1}}{{\mathfrak{p}}_{2}}$ in $K$. Let ${{E}_{{{p}^{n}}}}$ denote the ${{p}^{n}}$-division points on $E$. Assume that $F\left( {{E}_{{{p}^{n}}}} \right)$ is abelian over $K\,\text{for}\,\text{all}\,n\,\ge \,0$. This paper proves that the Pontrjagin dual of the $\mathfrak{p}_{1}^{\infty }$-Selmer group of $E$ over $F\left( {{E}_{{{p}^{\infty }}}} \right)$ is a finitely generated free $\wedge $-module, where $\wedge $ is the Iwasawa algebra of $\text{Gal}\left( F\left( {{E}_{{{p}^{\infty }}}} \right)/F\left( E\mathfrak{p}_{1}^{\infty }{{\mathfrak{p}}_{2}} \right) \right)$ . It also gives a simple formula for the rank of the Pontrjagin dual as a $\wedge $-module.

We consider the Neumann problem for the Schrödinger equations $-\Delta u\,+\,Vu\,=\,0$, with singular nonnegative potentials $V$ belonging to the reverse Hölder class ${{\mathcal{B}}_{n}}$ , in a connected Lipschitz domain $\Omega \,\subset \,{{\text{R}}^{n}}$ . Given boundary data $g$ in ${{H}^{p}}\text{or}\,{{L}^{p}}\,\text{for}\,\text{1}-\in \,<\,p\,\le \,2,\text{where}\,\text{0}<\in <\frac{1}{n}$ , it is shown that there is a unique solution, $u$, that solves the Neumann problem for the given data and such that the nontangential maximal function of $\nabla u$ is in ${{L}^{p}}(\partial \Omega )$. Moreover, the uniform estimates are found.

This paper is concerned with the Kirillov map for a class of torsion-free nilpotent groups $G$. $G$ is assumed to be discrete, countable and $\pi $-radicable, with $\pi $ containing the primes less than or equal to the nilpotence class of $G$. In addition, it is assumed that all of the characters of $G$ have idempotent absolute value. Such groups are shown to be plentiful.

We continue our investigation in [RST] of a martingale formed by picking a measurable set $A$ in a compact group $G$, taking random rotates of $A$, and considering measures of the resulting intersections, suitably normalized. Here we concentrate on the inverse problem of recognizing $A$ from a small amount of data from this martingale. This leads to problems in harmonic analysis on $G$, including an analysis of integrals of products of Gegenbauer polynomials.

In [6], Walter Philipp wrote that “… the law of the iterated logarithm holds for any process for which the Borel-Cantelli Lemma, the central limit theorem with a reasonably good remainder and a certain maximal inequality are valid.” Many authors [1], [2], [4], [5], [9] have followed this plan in proving the law of the iterated logarithm for sequences (or fields) of dependent random variables.

We carry on this tradition by proving the law of the iterated logarithm for a random field whose correlations satisfy an exponential decay condition like the one obtained by Spohn [8] for certain Gibbs measures. These do not fall into the $\phi $-mixing or strong mixing cases established in the literature, but are needed for our investigations [7] into diffusions on configuration space.

The proofs are all obtained by patching together standard results from [5], [9] while keeping a careful eye on the correlations.