Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T05:04:50.573Z Has data issue: false hasContentIssue false
  • English
  • Français

An Easy Proof for Some Classical Theorems in Plane Geometry

Published online by Cambridge University Press:  20 November 2018

C. Thas
C. Thas*
Affiliation:
Department of mathematics State University of Ghent Krijgslaan, 281 B-9000 Ghent Belgium
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result of this paper is a theorem about three conies in the complex or the real complexified projective plane. Is this theorem new? We have never seen it anywhere before. But since the golden age of projective geometry so much has been published about conies that it is unlikely that no one noticed this result. On the other hand, why does it not appear in the literature? Anyway, it seems interesting to "repeat" this property, because several theorems in connection with straight lines and (or) conies in projective, affine or euclidean planes are in fact special cases of this theorem. We give a few classical examples: the theorems of Pappus-Pascal, Desargues, Pascal (or its converse), the Brocard points, the point of Miquel. Finally, we have never seen in the literature a proof of these theorems using the same short method 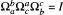see the proof of the main theorem).

Keywords

51A05 (51M05)
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 4 , 01 December 1992 , pp. 560 - 568
Copyright
Copyright © Canadian Mathematical Society 1992

References

Altschiller-Court, , College geometry: An introduction to the modern geometry of the triangle and the circle, Barnes and Noble, New-York, 1952.Google Scholar
Coxeter, H. S. M., The real projective plane, Cambridge University Press, 1961.Google Scholar
Evelyn, C. J. A., Money-Couts, G. B. and Tyrell, J. A., The seven circles theorem and other new theorems, Stacey international, London, 1974.Google Scholar
Pedoe, D., A course of geometry for colleges and universities, Cambridge University Press, 1970.Google Scholar