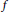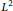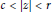Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Chunjie
and
Yang, Wenjie
2019.
Area integral means over the annuli.
Journal of Mathematical Analysis and Applications,
Vol. 473,
Issue. 1,
p.
510.
Hu, Qinxia
and
Wang, Chunjie
2020.
Convexity for area integral means.
Journal of Mathematical Analysis and Applications,
Vol. 491,
Issue. 2,
p.
124345.
段, 玉聪
2022.
Logarithmic Convexity of Area Integral Means.
Pure Mathematics,
Vol. 12,
Issue. 05,
p.
749.