Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T02:14:29.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Blow Analytic Mappings and Functions

Published online by Cambridge University Press:  20 November 2018

Etsuo Yoshinaga
Etsuo Yoshinaga*
Affiliation:
Department of Mathematics Faculty of Education Yokohama National University Hodogaya-ku Yokohama Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let π: M —> Rn be the blowing-up of Rn at the origin. Then a continuous map-germ f: (Rn — 0,0) —> Rm is called blow analytic if there exists an analytic map-germ 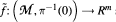such that 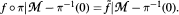Then an inverse mapping theorem for blow analytic mappings as a generalization of classical theorem is shown. And the following is shown. Theorem: The analytic family of blow analytic functions with isolated singularities admits an analytic trivialization after blowing-up.

Keywords

58C2758A07
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 4 , 01 December 1993 , pp. 497 - 506
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Bierstone, E. and Milman, P. D., Arc-analytic functions, Invent. Math. 101(1990), 411–424.Google Scholar
2. Fukui, T., The modified analytic trivialization of a family of real analytic mappings, Contemp. Math. 90(1989), 73–89.Google Scholar
3. Fukui, T. and Yoshinaga, E., The modified analytic trivialization of family of real analytic functions, Invent. Math. 82(1985), 467–477.Google Scholar
4. Kuo, T-C., The modified analytic trivialization of singularities, J. Math. Soc. Japan 32(1980), 605–614.Google Scholar
5. Kuo, T-C., On classification of real singularities, Invent. Math. 82(1985), 257–262.Google Scholar
6. Kuo, T-C., Ward, J. N., A theorem on almost analytic equisingularity,1. Math. Soc. Japan 33(1981), 471–484.Google Scholar
7. Suzuki, M., Stability of Newton diagrams of family of real analytic functions trivialized by blowing-up, Trans. Am. Math. Soc. 323(1991), 133–150.Google Scholar
8. Yoshinaga, E., The modified analytic trivialization of real analytic families via blowing-ups, J. Math. Soc. Japan 40(1988), 161–179.Google Scholar