Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T05:50:46.951Z Has data issue: false hasContentIssue false
  • English
  • Français

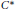${{C}^{*}}$-Algebras and Factorization Through Diagonal Operators

Published online by Cambridge University Press:  20 November 2018

Narcisse Randrianantoanina
Narcisse Randrianantoanina*
Affiliation:
Department of Mathematics and Statistics Miami University Oxford, Ohio 45056, e-mail: randrin@muohio.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 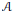$\mathcal{A}$ be a 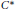${{C}^{*}}$-algebra and 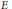$E$ be a Banach space with the Radon-Nikodym property. We prove that if 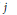$j$ is an embedding of 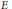$E$ into an injective Banach space then for every absolutely summing operator 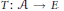$T:\,\mathcal{A}\,\to \,E$, the composition 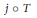$j\,\circ \,T$ factors through a diagonal operator from 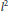${{l}^{2}}$ into 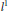${{l}^{1}}$. In particular, 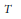$T$ factors through a Banach space with the Schur property. Similarly, we prove that for 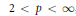$2\,<\,p\,<\,\infty $, any absolutely summing operator from 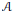$\mathcal{A}$ into 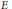$E$ factors through a diagonal operator from 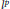${{l}^{p}}$ into 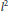${{l}^{2}}$.

Keywords

46L5047D15C*-algebrassumming operatorsdiagonal operatorsRadon-Nikodym property
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 4 , 01 December 2004 , pp. 615 - 623
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Diestel, J., Sequences and series in Banach spaces. Graduate Texts in Mathematics, 92, Springer-Verlag, New York, 1984.Google Scholar
[2] Diestel, J., Jarchow, H., and Tonge, A., Absolutely summing operators, Cambridge University Press, Cambridge, 1995.Google Scholar
[3] Diestel, J. and Uhl, J. J. Jr., Vector measures. Math. Surveys, 15, American Mathematical Society, Providence, R.I., 1977.Google Scholar
[4] Kadison, K. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. I: Elementary theory. Academic Press, New York, 1983.Google Scholar
[5] Kadison, K. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. II: Advanced theory. Academic Press, New York, 1986.Google Scholar
[6] Pietsch, A., Operator ideals. North-Holland, Amsterdam, 1980.Google Scholar
[7] Randrianantoanina, N., Factorization of operators on C*-algebras. Studia Math. 128 (1998), 273–285.Google Scholar
[8] Randrianantoanina, N., Absolutely summing operators on non commutative C*-algebras and applications. Houston J. Math. 25 (1999), 745–755.Google Scholar
[9] Randrianantoanina, N., Compact range property and operators on C*-algebras. Proc. Amer. Math. Soc. 129 (2001), 865–871.Google Scholar
[10] Saphar, P., Applications p décomposantes et p absolument sommantes. Israel J. Math. 11 (1972), 164–179.Google Scholar
[11] Takesaki, M., Theory of operator algebras. I. Springer-Verlag, New York, 1979.Google Scholar
[12] Upmeier, H., Symmetric Banach manifolds and Jordan C*-algebras. Notas de Matemática [Mathematical Notes], 96. North-Holland, Amsterdam, 1985.Google Scholar