Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T05:18:08.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Cesàro Operators on the Hardy Spaces of the Half-Plane

Published online by Cambridge University Press:  20 November 2018

Athanasios G. Arvanitidis  and
Aristomenis G. Siskakis
Athanasios G. Arvanitidis
Affiliation:
Department of Mathematics, University of Thessaloniki, 54124 Thessaloniki, Greece e-mail: arvanit@math.auth.grsiskakis@math.auth.gr
Aristomenis G. Siskakis
Affiliation:
Department of Mathematics, University of Thessaloniki, 54124 Thessaloniki, Greece e-mail: arvanit@math.auth.grsiskakis@math.auth.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we study the Cesàro operator

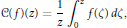$$C\left( f \right)\left( Z \right)=\frac{1}{Z}\int_{0}^{Z}{f\left( \zeta \right)d}\zeta,$$

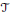and its companion operator $\mathcal{T}$ on Hardy spaces of the upper half plane. We identify 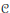$\mathcal{C}$ and 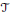$\mathcal{T}$ as resolvents for appropriate semigroups of composition operators and we find the norm and the spectrum in each case. The relation of 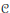$\mathcal{C}$ and 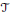$\mathcal{T}$ with the corresponding Cesàro operators on Lebesgue spaces 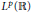${{L}^{p}}\left( \mathbb{R} \right)$ of the boundary line is also discussed.

Keywords

47B3830H1047D03Cesàro operatorsHardy spacessemigroupscomposition operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 229 - 240
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Brown, A., Halmos, P. R. and Shields, A. L., Cesáro operators. Acta Sci. Math. (Szeged) 26(1965) 125–137. Google Scholar
[2] Duren, P. L., Theory of Hp Spaces, Pure and Applied Mathematics, Vol. 38 Academic Press, New York-London 1970.Google Scholar
[3] Dunford, N. and Schwartz, J. T., Linear Operators, Part I, Pure and Applied Mathematics, Vol. 7 Interscience Publishers, Inc., New York, 1958.Google Scholar
[4] Garnett, J. B., Bounded Analytic Functions, Pure and Applied Mathematics, Vol. 96, Academic Press, Inc. New York-London, 1981.Google Scholar
[5] Hoffman, K., Banach Spaces of Analytic Functions, Reprint, Dover Publications, Inc., New York, 1988.Google Scholar
[6] Pazy, A., Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences, Vol. 44, Springer-Verlag, New York, 1983.Google Scholar
[7] Siskakis, A. G., Composition semigroups and the Cesáro operator on Hp. J. London Math. Soc. (2) 36 (1987), 153-164. http://dx.doi.org/10.1112/jlms/s2-36.1.153 Google Scholar