Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wyman, M.
1972.
Leo Moser 1921-1970.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 1,
p.
1.
Norton, Karl K.
1972.
On character sums and power residues.
Transactions of the American Mathematical Society,
Vol. 167,
Issue. 0,
p.
203.
BROUGHAN, KEVIN A.
2012.
ON SHIFTED PRIMES AND BALANCED PRIMES.
International Journal of Number Theory,
Vol. 08,
Issue. 08,
p.
2017.
Treviño, Enrique
2015.
The Burgess inequality and the least kth power non-residue.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1653.
Lapkova, Kostadinka
2018.
Correction to: Explicit upper bound for the average number of divisors of irreducible quadratic polynomials.
Monatshefte für Mathematik,
Vol. 186,
Issue. 4,
p.
675.
Bordellès, Olivier
2020.
Arithmetic Tales.
p.
159.
Balasubramanian, Ramachandran
Ramaré, Olivier
and
Srivastav, Priyamvad
2023.
Explicit bounds for products of primes in AP.
Mathematics of Computation,
Vol. 92,
Issue. 343,
p.
2381.


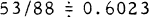 and
and 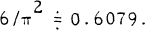 ) Our objective will be to examine R(x). In particular, we show that
) Our objective will be to examine R(x). In particular, we show that 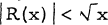 for all x and observe that
for all x and observe that 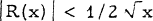 for x ≥ 8.
for x ≥ 8.