No CrossRef data available.
Article contents
Existence of Leray's Self-Similar Solutions of the Navier-Stokes Equations In 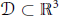 $\mathcal{D}\,\subset \,{{\mathbb{R}}^{3}}$
$\mathcal{D}\,\subset \,{{\mathbb{R}}^{3}}$
Published online by Cambridge University Press: 20 November 2018
Abstract
Leray's self-similar solution of the Navier-Stokes equations is defined by
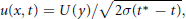 $$u(x,\,t)\,=\,U(y)/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},$$
$$u(x,\,t)\,=\,U(y)/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},$$
where 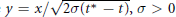 $y\,=\,x/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},\,\sigma \,>\,0$. Consider the equation for
$y\,=\,x/\sqrt{2\sigma ({{t}^{*}}\,-\,t)},\,\sigma \,>\,0$. Consider the equation for 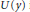 $U(y)$ in a smooth bounded domain
$U(y)$ in a smooth bounded domain 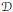 $\mathcal{D}$ of
$\mathcal{D}$ of 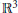 ${{\mathbb{R}}^{3}}$ with non-zero boundary condition:
${{\mathbb{R}}^{3}}$ with non-zero boundary condition:
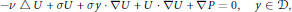 $$-v\,\Delta \,U\,+\,\sigma U\,+\,\sigma y\,\cdot \,\nabla U\,+\,U\,\cdot \,\nabla U\,+\,\nabla P\,=\,0,\,\,\,y\,\in \,\mathcal{D}\,$$
$$-v\,\Delta \,U\,+\,\sigma U\,+\,\sigma y\,\cdot \,\nabla U\,+\,U\,\cdot \,\nabla U\,+\,\nabla P\,=\,0,\,\,\,y\,\in \,\mathcal{D}\,$$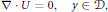 $$\nabla \,\cdot \,U\,=\,0,\,\,\,y\,\in \,\mathcal{D},$$
$$\nabla \,\cdot \,U\,=\,0,\,\,\,y\,\in \,\mathcal{D},$$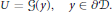 $$U\,=\,\mathcal{G}(y),\,\,\,y\,\in \,\partial \mathcal{D}.$$
$$U\,=\,\mathcal{G}(y),\,\,\,y\,\in \,\partial \mathcal{D}.$$
We prove an existence theorem for the Dirichlet problem in Sobolev space 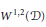 ${{W}^{1,2}}(\mathcal{D})$. This implies the local existence of a self-similar solution of the Navier-Stokes equations which blows up at
${{W}^{1,2}}(\mathcal{D})$. This implies the local existence of a self-similar solution of the Navier-Stokes equations which blows up at 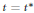 $t\,=\,{{t}^{*}}$ with
$t\,=\,{{t}^{*}}$ with 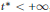 ${{t}^{*}}\,<\,+\infty $, provided the function
${{t}^{*}}\,<\,+\infty $, provided the function 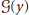 $\mathcal{G}(y)$ is permissible.
$\mathcal{G}(y)$ is permissible.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004


