Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T15:45:18.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Exotic Torsion, Frobenius Splitting and the Slope Spectral Sequence

Published online by Cambridge University Press:  20 November 2018

Kirti Joshi
Kirti Joshi*
Affiliation:
Mathematics Department, University of Arizona, 617 N. Santa Rita, Tucson, AZ 85721-0089, U.S.A. e-mail: kirti@math.arizona.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

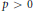In this paper we show that any Frobenius split, smooth, projective threefold over a perfect field of characteristic $p\,>\,0$ is Hodge–Witt. This is proved by generalizing to the case of threefolds a well-known criterion due to 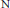$\text{N}$. Nygaard for surfaces to be Hodge-Witt. We also show that the second crystalline cohomology of any smooth, projective Frobenius split variety does not have any exotic torsion. In the last two sections we include some applications.

Keywords

14F3014J30threefoldsFrobenius splittingHodge–Wittcrystalline cohomologyslope spectral sequenceexotic torsion
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 567 - 578
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bloch, S., Torsion algebraic cycles and a theorem of Roitman. Compositio Math. 39(1979), no. 1, 107–127.Google Scholar
[2] Bloch, S., Lectures on Algebraic Cycles. Duke University Mathematics Series 4, Duke University, Mathematics Department, Durham, NC, 1980.Google Scholar
[3] Bloch, S. and Kato, K., p-adic étale cohomology. Inst. Hautes études Sci. Publ. Math. 63(1986), 107–152.Google Scholar
[4] Colliot-Thélène, J.-L., Sansuc, J.-J., and Soulé, C., Torsion dans le groupe de Chow de codimension deux. Duke Math. J. 50(1983), no. 3, 763–801, 1983.Google Scholar
[5] Deligne, P. and Illusie, L., Relévements modulo p 2 et decomposition du complexe de de Rham. Invent. Math. 89(1987), no. 2, 247–270.Google Scholar
[6] Ekedahl, T., On the multiplicative properties of the de Rham-Witt complex. I. Ark. Mat. 22(1984), no. 2, 185–239.Google Scholar
[7] Gros, M. and Suwa, N., Application d’Abel-Jacobi p-adique et cycles algébriques. Duke Math. J. 57(1988), no. 2, 579–613.Google Scholar
[8] Gros, M. and Suwa, N., Le conjecture de Gersten pour les faisceaux de Hodge-Witt logarithmique. Duke Math. J. 57(1988), no. 2, 615–628.Google Scholar
[9] Igusa, J.-I., On Some problems in abstract algebraic geometry. Proc. Nat. Acad. Sci. U. S. A. 41(1955), 964–967.Google Scholar
[10] Illusie, L., Complexe de de Rham-Witt et cohomologie cristalline. Ann. Scient. école Norm. Sup. 12(1979), no. 4, 501–661.Google Scholar
[11] Illusie, L. and Raynaud, M., Les suites spectrales associées au complexe de de Rham-Witt. Inst. Hautes Études Sci. Publ. Math. 57(1983), 73–212.Google Scholar
[12] Joshi, K. and Rajan, C. S., Frobenius splitting and ordinarity. Inter. Math. Res. Notices, 2003 no. 2, 109–121.Google Scholar
[13] Lakshmibai, V., Mehta, V. B., and Parmeswaran, A. J., Frobenius splittings and blow-ups. J. Algebra, 208(1998), no. 1, 101–128.Google Scholar
[14] Mehta, V. B. and Ramanathan, A., Frobenius splitting and cohomology vanishing for Schubert varieties. Ann. of Math. 122(1985), no. 1, 27–40.Google Scholar
[15] Mehta, V. B. and Srinivas, V., Varieties in positive characteristic with trivial tangent bundle. Compositio. Math. 64(1987), no. 2, 191–212.Google Scholar
[16] Merkur’ev, A. S. and Suslin, A. A., K-cohmology of Severi-Brauer varieties and the norm residue homomorphism. Izv. Akad. Nauk SSSr Ser. Mat. 46(1982), no. 5, 1011–1046.Google Scholar
[17] Nygaard, N., On the fundamental group of a unirational 3-fold. Invent. Math. 44(1978), no. 1, 75–86, 1978.Google Scholar
[18] Nygaard, N., Closedness of regular 1-forms on algebraic surfaces. Ann. Sci. École Norm. Sup. 12(1979), no. 1, 33–45.Google Scholar
[19] Schoen, C., On the geometry of a special determinantal hypersurface associated to the Mumford-Horrocks vector bundle. J. Reine Angew. Math. 364(1986), 85–111.Google Scholar
[20] Schoen, C., On the image of the ℓ-adic Abel-Jacobi map for a variety over the algebraic closure of a finite field. J. Amer.Math. Soc. 12(1999), no. 3, 795–838.Google Scholar
[21] Serre, J.-P., Sur la topologie des variétés algébriques en caractéristique p. In: Symposium internacional de topología algebraica. Universidad Nacional Autónoma de Mexico and UNESCO, Mexico, 1958, pp. 24–53.Google Scholar
[22] Shepherd-Barron, N., Fano threefolds in positive characteristic. Compositio Math. 105(1997), no. 3, 237–265.Google Scholar
[23] Srinivas, V., Decomposition of the de Rham complex. Proc. Indian Acad. Sci. Math. Sci. 100(1990), no. 2, 103–106.Google Scholar
[24] Suwa, N., Sur l’image de l’application d’Abel-Jacobi de Bloch. Bull. Soc. Math. France 116(1988), 69–101.Google Scholar