Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T17:12:43.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Inner E0-Semigroups on Infinite Factors

Published online by Cambridge University Press:  20 November 2018

Remus Floricel
Remus Floricel*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, U.S.A. e-mail: floricel@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the structure of inner 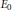${{E}_{0}}$-semigroups. We show that any inner 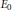${{E}_{0}}$-semigroup acting on an infinite factor 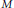$M$ is completely determined by a continuous tensor product system of Hilbert spaces in 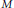$M$ and that the product system associated with an inner ${{E}_{0}}$-semigroup is a complete cocycle conjugacy invariant.

Keywords

46L4046L55von Neumann algebrassemigroups of endomorphismsproduct systemscocycle conjugacy
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 3 , 01 September 2006 , pp. 371 - 380
Copyright
Copyright © Canadian Mathematical Society 2006

References

[A1] Arveson, W., Continuous Analogues of Fock Space. Mem. Amer. Math. Soc. 80(1989), no. 409.Google Scholar
[A2] Arveson, W., E 0 -semigroups in quantum field theory. In: Quantization, Nonlinear Partial Differential Equations, And Operator Algebra, Proc. Sympos. Pure Math. 59, American Mathematical Society, Providence, RI, 1996, pp. 1–26.Google Scholar
[A3] Arveson, W., Noncommutative Dynamics and E-Semigroups. Springer-Verlag, New York, 2003.Google Scholar
[B] Bhat, B. V. R., Cocycles of CCR Flows. Memoirs of the American Mathematical Society 149, 2001, no. 709.Google Scholar
[C] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys. 57(1977), no. 2, 173–185.Google Scholar
[F1] Floricel, R., Endomorphisms of von Neumann Algebras. Thesis, Queen's University, Kingston, ON, 2002.Google Scholar
[F2] Floricel, R., A decomposition of E 0 -semigroups. In: Advances in Quantum Dynamics, Contemp. Math. 335, American Mathematical Society, Providence, RI, 2003, pp. 131–138.Google Scholar
[L] Longo, R., Simple injective subfactors. Adv. in Math. 63(1987), no. 2, 152–171.Google Scholar
[P1] Powers, R. T., A nonspatial continuous semigroup of *-endomorphisms of . Publ. Res. Inst. Math. Sci. 23(1987), no. 6, 1053–1069.Google Scholar
[P2] Powers, R. T., An index theory for semigroups of *-endomorphisms of and type II1 factors. Canad. J. Math. 40(1988), no. 1, 86–114.Google Scholar
[R] Roberts, J., Cross products of von Neumann algebras by group duals. Symposia Mathematica 20, Academic Press, London, 1976, pp. 335–363.Google Scholar