Instabilité de vecteurs propres d’opérateurs linéaires

Abstract

We consider some geometric properties of eigenvectors of linear operators on infinite dimensional Hilbert space. It is proved that the property of a family of vectors 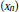$({{x}_{\text{n}}})$ to be eigenvectors 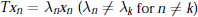$T{{x}_{n}}={{\lambda }_{n}}{{x}_{n}}({{\lambda }_{n}}\ne {{\lambda }_{k}}\text{for}\,n\ne k)$ of a bounded operator 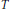$T$ (admissibility property) is very instable with respect to additive and linear perturbations. For instance, (1) for the sequence ${{\left( {{x}_{n}}+{{\epsilon }_{n}}{{v}_{n}} \right)}_{n\ge k(\epsilon )}}$ to be admissible for every admissible 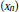$({{x}_{\text{n}}})$ and for a suitable choice of small numbers 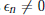${{\epsilon }_{n}}\,\ne \,0$ it is necessary and sufficient that the perturbation sequence be eventually scalar: there exist 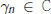${{\text{ }\!\!\gamma\!\!\text{ }}_{n}}\,\in \,C$ such that 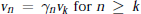${{v}_{n}}\,=\,{{\gamma }_{n}}{{v}_{k}}\,\text{for}\,n\,\ge \,\text{k}$ (Theorem 2); (2) for a bounded operator 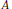$A$ to transform admissible families 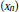$({{x}_{\text{n}}})$ into admissible families 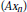$(A{{x}_{n}})$ it is necessary and sufficient that 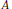$A$ be left invertible (Theorem 4).