Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T07:56:56.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix Characterizations of Topological Properties

Published online by Cambridge University Press:  20 November 2018

D.A. Bonnett  and
J.R. Porter
D.A. Bonnett
Affiliation:
University of Kansas
J.R. Porter
Affiliation:
University of Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

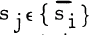In [S], H. Sharp characterizes each topology on a finite set S = {s1, s2,…sn} with a n×n zero-one matrix T = (tij) where tij=1 if and only if . In this paper we seek matrix characterizations of certain topological properties of finite spaces. Such characterizations will provide purely mechanical ways of determining if a space has a certain topological property.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 1 , April 1968 , pp. 95 - 105
Copyright
Copyright © Canadian Mathematical Society 1968

References

Aull, C.E. and Thron, W.J., Separation axioms between T and T Indagationes Mathematicae, 2 (1962), 26-37.Google Scholar
Davis, A.S., Indexed systems of neighborhoods for general topological spaces, Amer. Math. Monthly, 68, (1961), 886-893.10.1080/00029890.1961.11989785Google Scholar
Kelley, K J., General topology, Van Nostrand, New York, 1955.Google Scholar
Robinson, S. and Wu, Y. C., A note on separation axioms weaker than T1 , (to appear).10.1017/S1446788700005814Google Scholar
Sharp, H., Quasi-orderings and topologies on finite sets, Proc. Amer. Math. Soc., 17 (1966), 1344-1349.10.1090/S0002-9939-1966-0217771-XGoogle Scholar
Youngs, J.W.T., A note on separation axioms and their application in the theory of a locally connected topological space, Bull. Amer. Math. Soc., 49, (1943), 383-385.10.1090/S0002-9904-1943-07922-0Google Scholar