Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:54:27.203Z Has data issue: false hasContentIssue false
  • English
  • Français

New Super-quadratic Conditions for Asymptotically Periodic Schrödinger Equations

Published online by Cambridge University Press:  20 November 2018

Xianhua Tang
Xianhua Tang*
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, P.R. China. e-mail: tangxh@mail.csu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the semilinear Schrödinger equation

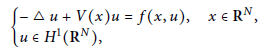$$\left\{ _{u\,\,\in \,\,{{H}^{1}}({{\mathbf{R}}^{N}}),}^{-\Delta \,u+V(x)u=f(x,u),\,\,\,\,\,x\in \,\,{{\mathbf{R}}^{N}},} \right.$$

where 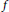$f$ is a superlinear, subcritical nonlinearity. It focuses on the case where 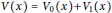$V(x)={{V}_{0}}(x)+{{V}_{1}}(x)$, 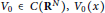${{V}_{0}}\in C({{\mathbf{R}}^{N}}),\,{{V}_{0}}(x)$ is 1-periodic in each of 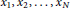${{x}_{1}},{{x}_{2}},...,{{x}_{N}}$, 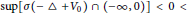$\sup [\sigma (-\Delta +{{V}_{0}})\,\cap \,(-\infty ,0)]<0<$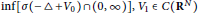$\inf [\sigma (-\Delta +{{V}_{0}})\cap (0,\infty )],\,{{V}_{1}}\in C({{\mathbf{R}}^{N}})$, and 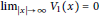${{\lim }_{|x|\to \infty }}\,{{V}_{1}}(x)=0$. A new super-quadratic condition is obtained that is weaker than some well-known results.

Keywords

35J2035J60Schrödinger equationsuperlinearasymptotically periodicground state solutions of Nehari-Pankov type
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 422 - 435
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Alama, S. and Li, Y. Y., On “multibump” bound states for certain semilinear elliptic equations. Indiana J. Math. 41(1992), no. 4, 983–1026. http://dx.doi.org/10.1512/iumj.1992.41.41052 Google Scholar
[2] Ambrosetti, A. and Rabinowitz, P. H., Dual variational methods in critical point theory and applications, J. Functional Anal. 14(1973), 349–381. http://dx.doi.org/1 0.101 6/0022-1236(73)90051-7 Google Scholar
[3] Bartsch, T. and Ding, Y. H., Solutions of nonlinear Dirac equations. J. Differ. Equations 226(2006), 210–249. http://dx.doi.org/10.1016/j.jde.2005.08.014 Google Scholar
[4] Bartsch, T. and Wang, Z.-Q., Existence and multiplicity results for some superlinear elliptic problems on RN. Comm. Partial Differential Equations 20(1995), 1725–1741. http://dx.doi.org/1 0.1080/03605309508821149 Google Scholar
[5] Coti Zelati, V. and Rabinowitz, P. H., Homoclinic type solutions for a semilinear elliptic PDE on RN. Comm. Pure Appl. Math. 45(1992), no. 10, 1217–1269. http://dx.doi.org/10.1 OO2/cpa.31 60451002 Google Scholar
[6] Ding, Y. and Lee, C., Multiple solutions of Schrôdinger equations with indefinite linear part and super or asymptotically linear terms. J. Differential Equations 222(2006) 137–163. http://dx.doi.org/10.1016/j.jde.2005.03.011 Google Scholar
[7] Ding, Y. and Luan, S. X., Multiple solutions for a class of nonlinear Schrôdinger equations. J. Differential Equations 207(2004), 423–457. http://dx.doi.org/10.1016/j.jde.2004.07.030 Google Scholar
[8] Ding, Y. and Szulkin, A., Bound states for semilinear Schrôdinger equations with sign-changing potential. Calc. Var. Partial Differential Equations 29(2007), no. 3, 397–419. http://dx.doi.org/10.1007/s00526-006-0071-8 Google Scholar
[9] Edmunds, D. E. and Evans, W. D., Spectral theory and differential operators. Clarendon Press, Oxford, 1987.Google Scholar
[10] Egorov, Y and Kondratiev, V., On spectral theory of elliptic operators. Operator Theory: Advances and Applications, 89. Birkhâuser Verlag, Basel, 1996. http://dx.doi.org/10.1007/978-3-0348-9029-8 Google Scholar
[11] Kryszewski, W. and Szulkin, A., Generalized linking theorem with an application to a semilinear Schrôdinger equation. Adv. Differ. Equations 3(1998), 441–472.Google Scholar
[12] Li, G. B. and Szulkin, A., An asymptotically periodic Schrôdinger equation with indefinite linear part. Commun. Contemp. Math. 4(2002). 763–776. http://dx.doi.org/10.1142/S0219199702000853 Google Scholar
[13] Li, Y Q., Wang, Z.-Q., and J. Zeng, Ground states of nonlinear Schrôdinger equations with potentials. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(2006), 829–837. http://dx.doi.org/10.1016/j.anihpc.2006.01.003 Google Scholar
[14] Lin, X. and Tang, X. H., Nehari-type ground state solutions for superlinear asymptotically periodic Schrôdinger equation. Abstr. Appl. Anal. (2014), ID 607078, 7. Google Scholar
[15] Lions, P. L., The concentration-compactness principle in the calculus of variations. The locally compact case. II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(1984), no. 4, 223–283. Google Scholar
[16] Liu, S., On superlinear Schrôdinger equations with periodic potential. Calc. Var. Partial Differential Equations 45(2012), 1–9. http://dx.doi.org/10.1007/s00526-011-0447-2 Google Scholar
[17] Liu, Z. L., and Z.-Q. Wang, On the Ambrosetti-Rabinowitz superlinear condition. Adv. Nonlinear Stud. 4(2004), no. 4, 561–572. http://dx.doi.org/10.1 51 5/ans-2004-0411 Google Scholar
[18] Pankov, A., Periodic nonlinear Schrôdinger equation with application to photonic crystals. Milan J. Math. 73(2005) 259–287. http://dx.doi.org/10.1007/s00032-005-0047-8 Google Scholar
[19] Rabinowitz, P. H., On a class of nonlinear Schrôdinger equations. Z. Angew. Math. Phys. 43(1992), 270–291. http://dx.doi.org/10.1007/BF00946631 Google Scholar
[20] Szulkin, A. and Weth, T., Ground state solutions for some indefinite variational problems. J. Funct. Anal. 257(2009), 3802–3822. http://dx.doi.org/10.1016/j.jfa.2009.09.013 Google Scholar
[21] Tang, X. H., Infinitely many solutions for semilinear Schrôdinger equations with sign-changing potential and nonlinearity. J. Math. Anal. Appl. 401(2013), 407–415. http://dx.doi.org/10.1016/j.jmaa.2012.12.035 Google Scholar
[22] Tang, X. H., New super-quadratic conditions on ground state solutions for superlinear Schrôdinger equation. Adv. Nonlinear Stud. 14(2014), 361–373. http://dx.doi.org/10.151 5/ans-2O14-0208 Google Scholar
[23] Tang, X. H., New conditions on nonlinearity for a periodic Schrôdinger equation having zero as spectrum. J. Math. Anal. Appl. 413(2014), 392–410. http://dx.doi.org/10.1016/j.jmaa.2O13.11.062 Google Scholar
[24] Tang, X. H., Non-Nehari manifold method for superlinear Schrôdinger equation. Taiwanese J. Math. 18(2014), 1957–1979.Google Scholar
[25] Tang, X. H., Non-Nehari manifold method for asymptotically linear Schrôdinger equation. J. Aust. Math. Soc. 98(2015), 104–116. http://dx.doi.org/! 0.101 7/S144678871 400041 X Google Scholar
[26] Tang, X. H., Non-Nehari manifold method for asymptotically periodic Schrodinger equations. Sci. ChinaMath. 58(2015), 715–728. http://dx.doi.org/10.1007/s11425-014-4957-1 Google Scholar
[27] Tang, X. H. and Cheng, B. T., Ground state sign-changing solutions for Kirchhofftype problems in bounded domains. J. Differential Equations 261(2016), 2384–2402 http://dx.doi.org/1 0.101 6/j.jde.2O1 6.04.032 Google Scholar
[28] Troestler, C. and Willem, M., Nontrivial solution of a semilinear Schrodinger equation. Commun. Partial Differ. Equ. 21(1996), 1431–1449. http://dx.doi.org/10.1080/03605309608821233 Google Scholar
[29] Willem, M., Minimax theorems. Progress in Nonlinear Differential Equations and their Applications, 24. Birkhâuser Boston, Boston, MA, 1996. http://dx.doi.org/10.1007/978-1-4612-4146-1 Google Scholar
[30] Willem, M. and Zou, W M., On a Schrodinger equation with periodic potential and spectrum point zero. Indiana Univ. Math. J. 52(2003), 109–132. http://dx.doi.org/10.1512/iumj.2OO3.52.2273 Google Scholar
[31] Yang, M., Ground state solutions for a periodic Schrodinger equation with superlinear nonlinearities. Nonlinear Anal. 72(2010), 2620–2627. http://dx.doi.org/10.1016/j.na.2009.11.009 Google Scholar
[32] Yang, M., W Chen, and Ding, Y. H., Solution of a class of Hamiltonian elliptic systems in K.N. J. Math. Anal. Appl. 362(2010), 338–349. http://dx.doi.org/10.1016/j.jmaa.2009.07.052 Google Scholar
[33] Zhang, H., Xu, J. X., and Zhang, F. B., Ground state solutions for asymptotically periodic Schrodinger equation with critical growth. Electron. J. Differential Equations 2013(2013), No.227,16pp. Google Scholar
[34] Zhang, R. M., J. Chen, and Zhao, F. K., Multiple solutions for superlinear elliptic systems of Hamiltonian type. Discrete. Contin. Dyn. Syst. Ser. A 30(2011), 1249–1262.Google Scholar