Hostname: page-component-6bf8c574d5-l72pf Total loading time: 0 Render date: 2025-03-09T21:40:12.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Best Approximation of |x|

Published online by Cambridge University Press:  20 November 2018

Colin Bennett ,
Karl Rudnick  and
Jeffrey D. Vaaler
Colin Bennett
Affiliation:
Dept. of Mathematics, McMaster University, 1280 Main St. West, Hamilton, Ont. L8S 4K1
Karl Rudnick
Affiliation:
Dept. of Mathematics, Texas A & M University, College Station, Texas 77843
Jeffrey D. Vaaler
Affiliation:
Dept. of Mathematics, The University of Texas, Austin, Texas 78712
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note the best uniform approximation on [—1,1] to the function |x| by symmetric complex valued linear fractional transformations is determined. This is a special case of the more general problem studied in [1]. Namely, for any even, real valued function f(x) on [-1,1] satsifying 0 = f ( 0 ) ≤ f (x) ≤ f (1) = 1, determine the degree of symmetric approximation

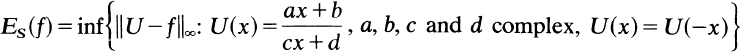
and the extremal transformations U whenever they exist.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 3 , 01 September 1979 , pp. 363 - 366
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Bennett, C., Rudnick, K., and Vaaler, J., Best uniform approximation by linear fractional transformations, Jour, of Approx. Th., to appear.Google Scholar
2. Bennett, C., Rudnick, K., and Vaaler, J., On a problem of Saff and Varga concerning best rational approximation, Padé and Rational Approximation, (E. B. Saff and R. S. Varga, ed.), Academic Press, 1977.Google Scholar
3. Ruttan, A., On the cardinality of a set of best complex rational approximations to a real function, Padé and Rational Approximations, (E. B. Saff and R. S. Varga, ed.), Academic Press, 1977.Google Scholar