Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:05:57.229Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Detecting Algebraic Cycles

Published online by Cambridge University Press:  20 November 2018

G. V. Ravindra
G. V. Ravindra*
Affiliation:
Department of Mathematics, Washington University, St. Louis, MO 63130, U.S.A. e-mail: ravindra@math.wustl.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to show that the homologically trivial cycles contructed by Clemens and their generalisations due to Paranjape can be detected by the technique of spreading out. More precisely, we associate to these cycles (and the ambient varieties in which they live) certain families which arise naturally and which are defined over 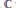$\mathbb{C}$ and show that these cycles, along with their relations, can be detected in the singular cohomology of the total space of these families.

Keywords

14C25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 3 , 01 September 2006 , pp. 464 - 471
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Asakura, M., Motives and algebraic de Rham cohomology. In: The Arithmetic and Geometry of Algebraic Cycles. CRM Proc. Lecture Notes 24, American Mathematical Society, Providence, RI, 2000, pp. 133–154,Google Scholar
[2] Biswas, J., Dayal, G., Paranjape, K. and Ravindra, G. V., Higher Abel–Jacobi maps. In: Algebra, Arithmetic and Geometry, Tata Inst. Fund. Res. Stud. Math. 16, Tata Inst. Fund. Res., Bombay, 2002, pp. 159–169.Google Scholar
[3] Colliot-Théléne, J.-L., Sansuc, J.-J. and Soulé, C., Torsion dans le groupe de Chow de codimension deux. Duke Math J. 50(1983), no. 3, 763–801.Google Scholar
[4] Clemens, H., Homological equivalence modulo algebraic equivalence is not finitely generated. Inst. Hautes Études Sci. Publ. Math. 58, (1983), 19–38.Google Scholar
[5] Esnault, H. and Viehweg, E., Deligne–Beilinson cohomology. In: Beilinson's Conjectures on Special Values of L-Functions, Perspect. Math. 4, Academic Press, Boston, MA, 1988, pp. 43–91.Google Scholar
[6] Jannsen, U., Mixed motives, motivic cohomology, and Ext-groups. Proceedings of the International Congress of Mathematicians, Birkhäuser, Basel, 1995, pp. 667–679.Google Scholar
[7] Lecomte, Florence, Rigidité des groupes de Chow. Duke Math. J. 53(1986), no. 2, 405–426.Google Scholar
[8] Lewis, J., A filtration on the Chow groups of a complex projective variety. Compositio Math. 128(2001), no. 3, 299–322.Google Scholar
[9] Merkurjev, A. S., and Suslin, A. A., K-cohomology of Severi–Brauer varieties and the norm residue homomorphism. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 46(1982), no. 5, 1011–1046, 1135–1136.Google Scholar
[10] Paranjape, K. H., Curves on 3-folds with trivial canonical bundle. Proc. Indian Acad. Sci. Math. Sci. 101(1991) no. 3, 199–213.Google Scholar
[11] Ravindra, G. V., Cohomological Detection of Algebraic Cycles, Thesis submitted to Madras University, 2001.Google Scholar
[12] Saito, M., Filtrations on Chow groups and transcendence degree. Publ. Res. Inst.Math. Sci. 40(2004), no. 3, 933–948.Google Scholar
[13] Srinivas, V., Gysin maps and cycle classes for Hodge cohomology. Proc. Indian Acad. Sci. Math. Sci. 103(1993), no. 3, 209–247.Google Scholar