Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eames, W.
1975.
On the Complete Regularity of Some Category Spaces.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 5,
p.
651.


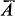 could be constructed for each subset
could be constructed for each subset 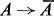 is a closure operator, and in this note some of the properties of the resulting topology are investigated. In particular, we obtain a sufficient condition for the space to be connected.
is a closure operator, and in this note some of the properties of the resulting topology are investigated. In particular, we obtain a sufficient condition for the space to be connected.