Published online by Cambridge University Press: 03 December 2018
We study the structure of the stable category 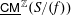 $\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ of graded maximal Cohen–Macaulay module over
$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ of graded maximal Cohen–Macaulay module over 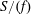 $S/(f)$ where
$S/(f)$ where 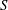 $S$ is a graded (
$S$ is a graded (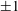 $\pm 1$)-skew polynomial algebra in
$\pm 1$)-skew polynomial algebra in  $n$ variables of degree 1, and
$n$ variables of degree 1, and 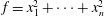 $f=x_{1}^{2}+\cdots +x_{n}^{2}$. If
$f=x_{1}^{2}+\cdots +x_{n}^{2}$. If 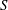 $S$ is commutative, then the structure of
$S$ is commutative, then the structure of 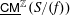 $\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is well known by Knörrer’s periodicity theorem. In this paper, we prove that if
$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is well known by Knörrer’s periodicity theorem. In this paper, we prove that if 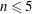 $n\leqslant 5$, then the structure of
$n\leqslant 5$, then the structure of 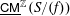 $\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is determined by the number of irreducible components of the point scheme of
$\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}(S/(f))$ is determined by the number of irreducible components of the point scheme of 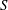 $S$ which are isomorphic to
$S$ which are isomorphic to 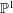 $\mathbb{P}^{1}$.
$\mathbb{P}^{1}$.
The author was supported by JSPS Grant-in-Aid for Early-Career Scientists 18K13381.