Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
and
Nowakowski, Richard J.
1997.
Monthly Unsolved Problems, 1969–1997.
The American Mathematical Monthly,
Vol. 104,
Issue. 10,
p.
967.
Kim, Jun Kyo
1998.
On Highly Factorable Numbers.
Journal of Number Theory,
Vol. 72,
Issue. 1,
p.
76.
Subbarao, M. V.
and
Verma, A.
2001.
Symbolic Computation, Number Theory, Special Functions, Physics and Combinatorics.
Vol. 4,
Issue. ,
p.
267.
Pyber, László
2004.
Groups of intermediate subgroup growth and a problem of Grothendieck.
Duke Mathematical Journal,
Vol. 121,
Issue. 1,
MANN, AVINOAM
2005.
A PROBABILISTIC ZETA FUNCTION FOR ARITHMETIC GROUPS.
International Journal of Algebra and Computation,
Vol. 15,
Issue. 05n06,
p.
1053.
KNOPFMACHER, A.
and
MAYS, M. E.
2005.
A SURVEY OF FACTORIZATION COUNTING FUNCTIONS.
International Journal of Number Theory,
Vol. 01,
Issue. 04,
p.
563.
Mann, Avinoam
2006.
Enumerating finite groups and their defining relations II.
Journal of Algebra,
Vol. 302,
Issue. 2,
p.
586.
De Wannemacker, Stefan
Laffey, Thomas
and
Osburn, Robert
2007.
On a conjecture of Wilf.
Journal of Combinatorial Theory, Series A,
Vol. 114,
Issue. 7,
p.
1332.
Hernane, Mohand-Ouamar
and
Nicolas, Jean-Louis
2007.
Grandes valeurs du nombre de factorisations d’un entier en produit ordonné de facteurs premiers.
The Ramanujan Journal,
Vol. 14,
Issue. 2,
p.
277.
Deléglise, M.
Hernane, M.O.
and
Nicolas, J.-L.
2008.
Grandes valeurs et nombres champions de la fonction arithmétique de Kalmár.
Journal of Number Theory,
Vol. 128,
Issue. 6,
p.
1676.
Lucchini, Andrea
2010.
On the subgroups with non-trivial Möbius number.
Journal of Group Theory,
Vol. 13,
Issue. 4,
Colombo, Valentina
and
Lucchini, Andrea
2010.
On subgroups with non-zero Möbius numbers in the alternating and symmetric groups.
Journal of Algebra,
Vol. 324,
Issue. 9,
p.
2464.
Lucchini, Andrea
2011.
Profinite groups with nonabelian crowns of bounded rank and their probabilistic zeta function.
Israel Journal of Mathematics,
Vol. 181,
Issue. 1,
p.
53.
Reddy, Shruthi
Sonker, Dheeraj
Singh, Pushpendra
Saxena, Komal
Singh, Surabhi
Chhajed, Rutuja
Tiwari, Samanyu
Karthik, K. V.
Ghosh, Subrata
Ray, Kanad
and
Bandyopadhyay, Anirban
2018.
Soft Computing Applications.
Vol. 761,
Issue. ,
p.
1.
Kumar, Abhimanyu
2023.
Investigation of norms of overpartitions.
The Ramanujan Journal,
Vol. 60,
Issue. 1,
p.
181.

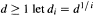 if
if 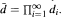 . Using a suitable generating function for
. Using a suitable generating function for