Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T13:41:41.125Z Has data issue: false hasContentIssue false
  • English
  • Français

On Surfaces with pg = 0 and K2 = 5

Published online by Cambridge University Press:  20 November 2018

Caryn Werner
Caryn Werner*
Affiliation:
Department of Mathematics, Allegheny College, Meadville, PA 16335 e-mail: cwerner@allegheny.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct new examples of surfaces of general type with 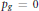${{P}_{g}}\,=\,0$ and 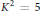${{K}^{2}}\,=\,5$ as ${{\mathbb{Z}}_{2}}\,\times \,{{\mathbb{Z}}_{2}}$-covers and show that they are genus three hyperelliptic fibrations with bicanonical map of degree two.

Keywords

14J29
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 746 - 756
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Borrelli, G., The classification of surfaces of general type with nonbirational bicanonical map. J. Algebraic Geom. 16(2007), no. 4, 625–669.Google Scholar
[2] Burniat, P., Sur les surfaces de genre P 12 > 1. Ann. Mat. Pura Appl.(4) 71(1996), 1– 24. doi:10.1007/BF02413731+1.+Ann.+Mat.+Pura+Appl.(4)+71(1996),+1–+24.+doi:10.1007/BF02413731>Google Scholar
[3] Catanese, F., Singular bidouble covers and the construction of interesting algebraic surfaces. In: Algebraic geometry: Hirzebruch 70, Contemp. Math., 241, Amer. Math. Soc., Providence, RI, 1999, pp. 97– 120.Google Scholar
[4] Du Val, P., On surfaces whose canonical system is hyperelliptic. Canadian J. Math. 4(1952), 204–221.Google Scholar
[5] Miyaoka, Y., Tricanonical maps of numerical Godeaux surfaces. Invent. Math 34(1976), no. 2, 99–111. doi:10.1007/BF01425477Google Scholar
[6] Lopes, M. Mendes and Pardini, R., Surfaces of general type with pg = 0, K 2 = 6 and non birational bicanonical map. Math. Ann. 329(2004), no. 3, 535–552.Google Scholar
[7] Lopes, M. Mendes and Pardini, R., A connected component of the moduli space of surfaces with pg = 0. Topology 40(2001), no. 5, 977–991. doi:10.1016/S0040-9383(00)00004-5Google Scholar
[8] Reider, I., Vector bundles of rank 2 and linear systems on algebraic surfaces. Ann. of Math. 127(1988), no. 2, 309–316. (1988). doi:10.2307/2007055Google Scholar
[9] Xiao, G., Degree of the bicanonical map of a surface of general type. Amer. J. Math. 112(1990), no. 5, 713–736. doi:10.2307/2374804Google Scholar