Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yue, Zhang Nan
and
Williams, Kenneth S.
1993.
Some Series Representations of $\z(2n+1)$.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 4,
Ewell, John A.
1995.
On the Zeta Function Values $\z(2k+1)$, $k=1,2,\ldots$.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 3,
Chen, Ming-Po
and
Srivastava, H.M.
1998.
Some Families of Series Representations for the Riemann ζ(3).
Results in Mathematics,
Vol. 33,
Issue. 3-4,
p.
179.
Dancs, Michael J.
and
He, Tian-Xiao
2006.
Numerical approximation to ζ(2n+1).
Journal of Computational and Applied Mathematics,
Vol. 196,
Issue. 1,
p.
150.
2012.
Zeta and q-Zeta Functions and Associated Series and Integrals.
p.
603.


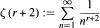
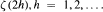 Thus, the set
Thus, the set 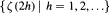 serves as a kind of basis for expressing all of the values
serves as a kind of basis for expressing all of the values