Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T02:14:04.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic Solutions For ẋ = Ax + G(x, t) + ∊p(t)

Published online by Cambridge University Press:  20 November 2018

Peter J. Ponzo
Peter J. Ponzo*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We wish to establish the existence of a periodic solution to

1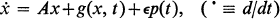

where x, g and p are n-vectors, A is an n × n constant matrix, and ∊ is a small scalar parameter. We assume that g and p are locally Lipschitz in x and continuous and T-periodic in t, and that the origin is a point of asymptotically stable equilibrium, when ∊ = 0.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 4 , December 1971 , pp. 575 - 577
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Cesari, L., Asymptotic behaviour and stability problems in ordinary differential equations, Springer-Verlag, Berlin (1963), 115-182.Google Scholar
2. Freedman, H. I., Estimates on the existence region for periodic solutions of equations involving a small parameter, SIAM J. Appl. Math. 16 (1968), 1341-1349.Google Scholar