Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T07:54:50.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudo-Integrality

Published online by Cambridge University Press:  20 November 2018

David F. Anderson ,
Evan G. Houston  and
Muhammad Zafrullah
David F. Anderson
Affiliation:
Department of Mathematics University of Tennessee Knoxville, Tennessee 37996-1300
Evan G. Houston
Affiliation:
Department of Mathematics University of North Carolina at Charlotte Charlotte, NC 28223
Muhammad Zafrullah
Affiliation:
Department of Mathematics University of Iowa Iowa City, IA 52242
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be an integral domain. An element u of the quotient field of R is said to be pseudo-integral over R if uIv ⊆ Iv for some nonzero finitely generated ideal I of R. The set of all pseudo-integral elements forms an integrally closed (but not necessarily pseudo-integrally closed) overling R ofR. It is shown that 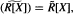, where X is a family of indeterminates; pseudo-integrality is analyzed in rings of the form D + M; and an example is given to show that pseudo-integrality does not behave well with respect to localization.

Keywords

13G0513B2013F05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 34 , Issue 1 , 01 March 1991 , pp. 15 - 22
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Anderson, D. F. and Ryckaert, A., The class group of D + M, J. Pure Appl. Algebra 52 (1988), 199–212.Google Scholar
2. Barucci, V., Anderson, D. F. and Dobbs, D. E., Coherent Mori domains and the principal ideal theorem, Comm. Algebra 15( 1987), 1119–1156.Google Scholar
3. Bastida, E. and Gilmer, R., Overrings and divisorial ideals of rings of the form D + M, Michigan Math. J. 20 (1973), 79–95.Google Scholar
4. Barucci, V. and Gabelli, S., How far is a Mori domain from being a Krull domain?, J. Pure Appl. Algebra 45 (1987), 101–112.Google Scholar
5. Dobbs, D., Houston, E., Lucas, T. and Zafrullah, M., t-linked overrings and Prüfer v-multiplication domains, Comm. Algebra 17 (1989), 2835–2852.Google Scholar
6. Gilmer, R., Multiplicative ideal theory. Dekker, New York, 1972.Google Scholar
7. Gilmer, R., Commutative semigroup rings, The University of Chicago Press, Chicago and London, 1984.Google Scholar
8. Gilmer, R. and Heinzer, W., On the complete integral closure of an integral domain, J. Aust. Math. Soc. 6 (1966), 351–361.Google Scholar
9. Glaz, S. and Vasconcelos, W., Flat ideals III, Comm. Alg. 12 (1984), 199–227.Google Scholar
10. Heinzer, W., An essential integral domain with a non-essential localization, Can. J. Math. 33(1981), 400– 403.Google Scholar
11. Houston, E. and Zafrullah, M., On t-vertibility II, Comm. Algebra 17 (1989), 1955–1969.Google Scholar
12. Kang, B. G., *-operations on integral domains, Ph.D. Thesis, The University of Iowa, 1987.Google Scholar
13. Nagata, M., On Krull's conjecture concerning valuation rings, Nagoya Math. J. 4 (1952), 29–33.Google Scholar
14. Nagata, M., Corrections to my paper “On Krull's conjecture concerning valuation rings”, Nagoya Math. J. 9 (1955), 201–212.Google Scholar
15. Northcott, D. G., A generalization of a theorem on the content ofpolynomials, Proc. Cambridge Phil. Soc. 55 (1959), 282–288.Google Scholar
16. Querré, J., Sur une propriété des anneaux de Krull, Bull. Soc. Math (2de série)95 (1971), 341–354.Google Scholar
17. Sheldon, P., Two counterexamples involving complete integral closure in finite-dimensional Priifer domains, J. Algebra 27 (1973), 462–474.Google Scholar
18. van der Waerden, B. L., Modern algebra, 2nd English éd., vol. 2, Ungar, New York, 1950.Google Scholar
19. Zafrullah, M., On finite conductor domains, Manuscripta Math. 24 (1978), 191–203.Google Scholar
20. Zafrullah, M., Ascending chain conditions and star operations, Comm. Algebra 17 (1989), 1523–1533.Google Scholar