Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T05:27:23.345Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramsey Number of Wheels Versus Cycles and Trees

Published online by Cambridge University Press:  20 November 2018

Ghaffar Raeisi  and
Ali Zaghian
Ghaffar Raeisi
Affiliation:
Department of Mathematical Sciences, Shahrekord University, Shahrekord, P.O. Box 115, Iran e-mail: g.raeisi@math.iut.ac.ir
Ali Zaghian
Affiliation:
Department of Mathematics and Cryptography, Malek-Ashtar University of Technology, Isfahan, P.O. Box 83145/115, Iran e-mail: a.zaghian@mut-es.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 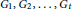${{G}_{1}},\,{{G}_{2}},\,.\,.\,.\,,\,{{G}_{t}}$ be arbitrary graphs. The Ramsey number 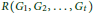$R\left( {{G}_{1}},\,{{G}_{2}},\,.\,.\,.,{{G}_{t}} \right)$ is the smallest positive integer $n$ such that if the edges of the complete graph 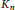${{K}_{n}}$ are partitioned into $t$ disjoint color classes giving $t$ graphs 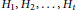${{H}_{1}},\,{{H}_{2}},\,.\,.\,.\,,\,{{H}_{t}}$ , then at least one 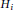${{H}_{i}}$ has a subgraph isomorphic to 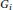${{G}_{i}}$ . 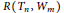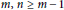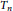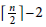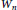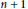In this paper, we provide the exact value of the $R({{T}_{n}},\,{{W}_{m}})$ for odd $m,\,n\,\ge \,m-1$ , where ${{T}_{n}}$ is either a caterpillar, a tree with diameter at most four, or a tree with a vertex adjacent to at least $\left\lceil \frac{n}{2} \right\rceil \,-\,2$ leaves, and ${{W}_{n}}$ is the wheel on $n\,+\,1$ vertices. Also, we determine 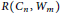$R\left( {{C}_{n}},\,{{W}_{m}} \right)$ for even integers $n$ and 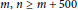$m,\,n\,\ge \,m\,+\,500$ , which improves a result of Shi and confirms a conjecture of Surahmat et al. In addition, the multicolor Ramsey number of trees versus an odd wheel is discussed in this paper.

Keywords

05C1505C5505C65Ramsey numberwheeltreecycle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 190 - 196
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bondy, J. A. and Murty, U. S. R., Graph theory with applications. American Elsevier Publishing Co. Inc., New York, 1976.Google Scholar
[2] Baskoro, E. T., Surahmat, Nababan, S. M., and Miller, M.. On Ramsey numbers for trees versus wheels of five or six vertices. Graphs Combin. 18(2002), 717–721. http://dx.doi.Org/10.1007/S003730200056 Google Scholar
[3] Brandt, S., Faudree, R.. and Goddard, W.. Weakly pancydic graphs. J. Graph Theory 27(1998), 141–176. http://dx.doi.Org/10.1002/(SICI)1097-0118(199803)27:3141::AID-JGT33.0.CO;2-O Google Scholar
[4] Burr, S. A. and Roberts, J. A., On Ramsey numbers for stars. Util. Math. 4(1973), 217–220.Google Scholar
[5] Chen, Y., Zhang, Y.. and Zhang, K.. The Ramsey numbers of paths versus wheels. Discrete Math. 290(2005), 85–87. http://dx.doi.Org/10.101 6/j.disc.2004.10.01 7 Google Scholar
[6] Dirac, G. A., Some theorems on abstract graphs. Proc. London Math. Soc. 2(1952), 69–81. http://dx.doi.Org/10.1112/plms/s3-2.1.69 Google Scholar
[7] Eaton, N. and Tiner, G.. On the Erdôs and Sôs conjecture and graphs with large minimum degree. Ars Combin. 95(2010), 373–382.Google Scholar
[8] Erdôs, P. and Gallai, T.. On maximal paths and circuits of graphs. Acta Math. Acad. Sci. Hungar. 10(1959), 337–356. http://dx.doi.Org/10.1007/BF02024498 Google Scholar
[9] Faudree, R. J. and Schelp, R. H., All Ramsey numbers for cycles in graphs. Discrete Math. 8(1974), 313-329. http://dx.doi.Org/10.1016/0012-365X(74)90151-4 Google Scholar
[10] Moser, W. and Pach, J.. Recent developments in combinatorial geometry. In: New trends in discrete and computational geometry, Algorithms Combin., 10, Springer, Berlin, 1993.Google Scholar
[11] McLennan, A., The Erdôs and S6s conjecture for trees of diameter four. J. Graph Theory 49(2005), 291–301. http://dx.doi.Org/10.1 OO2/jgt.2OO83 Google Scholar
[12] Radziszowski, S. P., Small Ramsey numbers. Electronic J. Combin. 1(1994), Dynamic Surveys, DS1.12 (August 4, 2009).Google Scholar
[13] Ramsey, F. P., On a problem of formal logic. Proc. London Math. Soc. (2) 30(1930), 264–286. http://dx.doi.Org/10.1112/plms/s2-30.1.264 Google Scholar
[14] Shi, L., Ramsey numbers of long cycles versus books or wheels. European J. Combin. 31(2010), 828–838. http://dx.doi.Org/10.1016/j.ejc.2009.07.004 Google Scholar
[15] Surahmat, E.T. Baskoro, and Broersma, H. J., The Ramsey numbers of large cycles versus small wheels. Integers 4(2004), AlO.Google Scholar
[16] Surahmat, E.T. Baskoro, and Tomescu, I., The Ramsey numbers of large cycles versus odd wheels. Graphs Combin. 24(2008), 53–58. http://dx.doi.Org/10.1007/s00373-007-0764-6 Google Scholar
[17] Surahmat, E.T. Baskoro, The Ramsey numbers of large cycles versus wheels. Discrete Math. 306(2006), 3334–3337. http://dx.doi.Org/! 0.101 6/j.disc.2006.06.006 Google Scholar