Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:25:01.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of Compact Right Topological Groups

Published online by Cambridge University Press:  20 November 2018

Paul Milnes
Paul Milnes*
Affiliation:
University of Western Ontario London, Ontario N6A 5B7
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Compact right topological groups arise naturally as the enveloping semigroups of distal flows. Recently, John Pym and the author established the existence of Haar measure μ on such groups, which invites the consideration of the regular representations. We start here by characterizing the continuous representations of a compact right topological group G, and are led to the conclusion that the right regular representation r is not continuous (unless G is topological). The domain of the left regular representation l is generally taken to be the topological centre

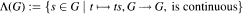
or a tractable subgroup of it, furnished with a topology stronger than the relative topology from G (the goals being to have l both defined and continuous). An analysis of l and r on H = L2(G) for some non-topological compact right topological groups G shows, among other things, that:

  1. (i) for the simplest (perhaps) G generated by ℤ, (l, H) decomposes into one copy of each irreducible representation of ℤ and c copies of the regular representation.

  2. (ii) for the simplest (perhaps) G generated by the euclidean group of the plane , (l, H) decomposes into one copy of each of the continuous one-dimensional representations of and c copies of each continuous irreducible representation Ua,a > 0.

  3. (iii) when Λ(G) is not dense in G, it can seem very reasonable to regard r as a continuous representation of a related compact topological group, and also, G can be almost completely "lost" in the measure space (G, μ).

Keywords

22D10compact right topological groupHaar measureregular representation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 3 , 01 September 1993 , pp. 314 - 323
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Anzai, H. and Kakutani, S., Bohr compactifications of a locally compact abelian group I, II, Proc. Imp. Acad. Tokyo 19(1943), 476–480,533-539.Google Scholar
2. Berglund, J. F., Junghenn, H. D. and Milnes, P., Analysis on Semigroups: Function Spaces, Compactifications, Representations, Wiley, New York, 1989.Google Scholar
3. Dixmier, J., Les C*-algebras et leurs représentations, Gauthier-Villars, Paris, 1964.Google Scholar
4. Ellis, R., Locally compact transformation groups, Duke Math. J. 24(1957), 119–126.Google Scholar
5. Ellis, R., Distal transformation groups, Pacific J. Math. 9(1958), 401–405.Google Scholar
6. Ellis, R., Lectures on Topological Dynamics, Benjamin, New York, 1969.Google Scholar
7. Furstenberg, H., The structure of distal flows, Amer. J. Math. 85(1963), 477–515.Google Scholar
8. Hewitt, E. and Ross, K. A., Abstract Harmonie Analysis I, Springer-Verlag, New York, 1963.Google Scholar
9. Loomis, L. H., An Introduction to Abstract Harmonie Analysis, Van Nostrand, New York, 1953.Google Scholar
10. Milnes, P., Distal compact right topological groups Acta Math. Hung., to appear..Google Scholar
11. Milnes, P. and A. Paterson, L. T., Ergodic sequences and a subspace ofB(G), Rocky Mountain J. Math. 18(1988), 681–694.Google Scholar
12. Milnes, P. and Pym, J., Haar measure for compact right topological groups, Proc. Amer. Math. Soc, 114(1992), 387–393.Google Scholar
13. Milnes, P. and Pym, J., Homomorphisms of minimal and distal flows, to appear.Google Scholar
14. Namioka, I., Right topological groups, distal flows and a fixed point theorem, Math. Systems Theory 6(1972), 193–209.Google Scholar
15. Namioka, I., Ellis groups and compact right topological groups. In: Contemporary Mathematics, Conference in Modern Analysis and Probability, Amer. Math. Soc. 26(1984), 295–300.Google Scholar
16. Ruppert, W., Uber kompakte rechtstopologische Gruppen mit gleichgradig stetigen Linkstranslationen, Sitzungsberichten der Ôsterreichischen Akademie der Wissenschaften Mathem.-naturw. Klasse, Abteilung 11184(1975), 159–169.Google Scholar
17. Sigiura, M., Unitary Representations and Harmonic Analysis, Wiley, New York, 1975.Google Scholar