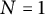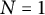1 Introduction
Harish-Chandra modules play important roles in the representation theory of Lie algebras and Lie superalgebras. They are characterized by certain algebraic properties that make them amenable to the study of the asymptotic behavior of the corresponding Lie group or Lie supergroup. In various Lie superalgebras such as the
![]() $N=1$
Ramond algebra in [Reference Cai, Liu and Lü7] and the Witt superalgebra in [Reference Billig, Futorny, Iohara and Kashuba6, Reference Xue and Lü23], the classifications of such modules have been completed through the use of the A cover theory introduced in [Reference Billig and Futorny5]. These Lie superalgebras are all
$N=1$
Ramond algebra in [Reference Cai, Liu and Lü7] and the Witt superalgebra in [Reference Billig, Futorny, Iohara and Kashuba6, Reference Xue and Lü23], the classifications of such modules have been completed through the use of the A cover theory introduced in [Reference Billig and Futorny5]. These Lie superalgebras are all
![]() ${\mathbb Z}$
-graded. However, the task of classifying all simple jet modules for
${\mathbb Z}$
-graded. However, the task of classifying all simple jet modules for
![]() $\frac 12{\mathbb Z}$
-graded Lie superalgebras is more complicated, as demonstrated in [Reference Cai and Lü8] for the case of the
$\frac 12{\mathbb Z}$
-graded Lie superalgebras is more complicated, as demonstrated in [Reference Cai and Lü8] for the case of the
![]() $N=1$
Neveu-Schwarz algebra.
$N=1$
Neveu-Schwarz algebra.
This paper appears to be focused on the study of the representation theory of the
![]() $N=1$
Heisenberg–Virasoro superalgebra
$N=1$
Heisenberg–Virasoro superalgebra
![]() $\mathfrak g$
(a kind of superconformal current algebra), which is a Lie superalgebra that arises in the context of mathematical physics and theoretical physics [Reference Kac and Todorov12]. It is a supersymmetric extension of the twisted Heisenberg–Virasoro algebra. This algebra can be realized from Balinsky–Novikov superalgebras, which construct local translation invariant Lie superalgebras of vector-valued functions on the line, as described in [Reference Pei and Bai20]. The Verma modules, Whittaker modules, and smooth modules over
$\mathfrak g$
(a kind of superconformal current algebra), which is a Lie superalgebra that arises in the context of mathematical physics and theoretical physics [Reference Kac and Todorov12]. It is a supersymmetric extension of the twisted Heisenberg–Virasoro algebra. This algebra can be realized from Balinsky–Novikov superalgebras, which construct local translation invariant Lie superalgebras of vector-valued functions on the line, as described in [Reference Pei and Bai20]. The Verma modules, Whittaker modules, and smooth modules over
![]() $\mathfrak g$
are studied in several papers [Reference Adamović, Jandrić and Radobolja1, Reference Adamovic, Jandric and Radobolja2, Reference Liu, Pei, Xia and Zhao15]. Drawing on the research conducted on the
$\mathfrak g$
are studied in several papers [Reference Adamović, Jandrić and Radobolja1, Reference Adamovic, Jandric and Radobolja2, Reference Liu, Pei, Xia and Zhao15]. Drawing on the research conducted on the
![]() $N=1$
Neveu-Schwarz algebra in [Reference Cai and Lü8] and the Ovsienko-Roger superalgebra in [Reference Dilxat, Chen and Liu10], this paper classifies all simple Harish-Chandra modules over
$N=1$
Neveu-Schwarz algebra in [Reference Cai and Lü8] and the Ovsienko-Roger superalgebra in [Reference Dilxat, Chen and Liu10], this paper classifies all simple Harish-Chandra modules over
![]() $\mathfrak g$
using methods developed in [Reference Liu, Pei and Xia14]. Note that our methods here are appropriate to the
$\mathfrak g$
using methods developed in [Reference Liu, Pei and Xia14]. Note that our methods here are appropriate to the
![]() ${\mathbb Z}$
-graded and
${\mathbb Z}$
-graded and
![]() $\frac 12{\mathbb Z}$
-graded superconformal current algebras. Such researches for the
$\frac 12{\mathbb Z}$
-graded superconformal current algebras. Such researches for the
![]() ${\mathbb Z}$
-graded superconformal current algebra were completed in [Reference He, Liu and Wang11] by the A-cover theory, which cannot be refer to the
${\mathbb Z}$
-graded superconformal current algebra were completed in [Reference He, Liu and Wang11] by the A-cover theory, which cannot be refer to the
![]() $\frac 12{\mathbb Z}$
case.
$\frac 12{\mathbb Z}$
case.
To study tensor products of well-known modules is a basic task in representation theory of Lie (super)algebras. Recently, the tensor products of highest weight modules and Harish-Chandra modules of the intermediate series, which are not Harish-Chandra modules, over the Virasoro algebra, the twisted Heisenberg–Virasoro algebra, and the super Virasoro algebra, the Schrödinger-Virasoro algebra were studied in [Reference Chen, Guo and Zhao9, Reference Liu and Zhang16, Reference Lü and Zhao18, Reference Zhang25, Reference Zhang26], etc. In this paper, we solve this problem for the
![]() $N=1$
Heisenberg–Virasoro superalgebra with singular vectors constructed in [Reference Adamović, Jandrić and Radobolja1, Reference Adamovic, Jandric and Radobolja2]. The necessary and sufficient conditions for these tensor products to be simple are studied and an isomorphism theorem for such tensor products is given.
$N=1$
Heisenberg–Virasoro superalgebra with singular vectors constructed in [Reference Adamović, Jandrić and Radobolja1, Reference Adamovic, Jandric and Radobolja2]. The necessary and sufficient conditions for these tensor products to be simple are studied and an isomorphism theorem for such tensor products is given.
The paper is organized as follows: Section 2 presents basic results for our study, Sections 3 and 4 classify all simple Harish-Chandra modules (Theorems 3.2, 4.3). The necessary and sufficient conditions for the tensor product of the highest weight modules, and the modules of the intermediate series over
![]() $\mathfrak g$
to be simple are studied (Theorem 6.6) and an isomorphism theorem (Theorem 6.8) for such tensor products is given in Sections 5 and 6.
$\mathfrak g$
to be simple are studied (Theorem 6.6) and an isomorphism theorem (Theorem 6.8) for such tensor products is given in Sections 5 and 6.
Throughout this paper, we will use the following notations:
![]() ${\mathbb C}$
,
${\mathbb C}$
,
![]() ${\mathbb N}$
,
${\mathbb N}$
,
![]() ${\mathbb Z}_+$
, and
${\mathbb Z}_+$
, and
![]() ${\mathbb Z}$
refer to the sets of complex numbers, nonnegative integers, positive integers, and integers, respectively.
${\mathbb Z}$
refer to the sets of complex numbers, nonnegative integers, positive integers, and integers, respectively.
2 Preliminaries
In this section, we recall some definitions and results for later use.
2.1 Basic definitions
Let
![]() $V = V_{\bar 0}\oplus V_{\bar 1}$
be any
$V = V_{\bar 0}\oplus V_{\bar 1}$
be any
![]() ${\mathbb Z}_2$
-graded vector space. Then any element
${\mathbb Z}_2$
-graded vector space. Then any element
![]() $u\in V_{\bar 0}$
(
$u\in V_{\bar 0}$
(
![]() $\mathrm {resp. }$
$\mathrm {resp. }$
![]() $u\in V_{\bar 1}$
) is said to be even (
$u\in V_{\bar 1}$
) is said to be even (
![]() $\mathrm {resp.}$
odd). We define
$\mathrm {resp.}$
odd). We define
![]() $\bar u=0$
if u is even and
$\bar u=0$
if u is even and
![]() $\bar u=1$
if u is odd. Elements in
$\bar u=1$
if u is odd. Elements in
![]() $V_{\bar 0}$
or
$V_{\bar 0}$
or
![]() $V_{\bar 1}$
are called homogeneous. Whenever
$V_{\bar 1}$
are called homogeneous. Whenever
![]() $\bar u$
is written, it is understood that u is homogeneous.
$\bar u$
is written, it is understood that u is homogeneous.
Let
![]() $L=L_{\bar 0}\oplus L_{\bar 1}$
be a Lie superalgebra, an L-module is a
$L=L_{\bar 0}\oplus L_{\bar 1}$
be a Lie superalgebra, an L-module is a
![]() ${\mathbb Z}_2$
-graded vector space
${\mathbb Z}_2$
-graded vector space
![]() $V=V_{\bar 0}\oplus V_{\bar 1}$
together with a bilinear map,
$V=V_{\bar 0}\oplus V_{\bar 1}$
together with a bilinear map,
![]() $L\times V\to V$
, denoted
$L\times V\to V$
, denoted
![]() $(x,v)\mapsto xv$
such that
$(x,v)\mapsto xv$
such that
for all
![]() $x,y\in L, v\in V$
, and
$x,y\in L, v\in V$
, and
![]() $L_{i} V_{j}\subseteq V_{i+j}$
for all
$L_{i} V_{j}\subseteq V_{i+j}$
for all
![]() $i, j\in {\mathbb Z}_2$
. It is clear that there is a parity change functor
$i, j\in {\mathbb Z}_2$
. It is clear that there is a parity change functor
![]() $\Pi $
on the category of L-modules, which interchanges the
$\Pi $
on the category of L-modules, which interchanges the
![]() ${\mathbb Z}_2$
-grading of a module. We use
${\mathbb Z}_2$
-grading of a module. We use
![]() $U(L)$
to denote the universal enveloping algebra of the Lie superalgebra L.
$U(L)$
to denote the universal enveloping algebra of the Lie superalgebra L.
2.2 The
 $N=1$
Heisenberg–Virasoro superalgebra
$N=1$
Heisenberg–Virasoro superalgebra
Definition 2.1 [Reference Kac and Todorov12]
The
![]() $N=1$
Heisenberg–Virasoro superalgebra
$N=1$
Heisenberg–Virasoro superalgebra
![]() $\mathfrak g:={\mathfrak g}_{\bar 0}+{\mathfrak g}_{\bar 1}$
, where
$\mathfrak g:={\mathfrak g}_{\bar 0}+{\mathfrak g}_{\bar 1}$
, where
![]() ${\mathfrak g}_{\bar 0}:={\mathbb C}\{L_m, H_m, C_1, C_2, C_3\mid m\in {\mathbb Z}\}$
and
${\mathfrak g}_{\bar 0}:={\mathbb C}\{L_m, H_m, C_1, C_2, C_3\mid m\in {\mathbb Z}\}$
and
![]() ${\mathfrak g}_{\bar 1}={\mathbb C}\{G_p, F_p\mid p\in {\mathbb Z}+\frac 12\}$
, with the following relations:
${\mathfrak g}_{\bar 1}={\mathbb C}\{G_p, F_p\mid p\in {\mathbb Z}+\frac 12\}$
, with the following relations:
 $$ \begin{align*} & [L_m,L_n]=(n-m)L_{n+m}+\delta_{m+n, 0}{1\over12}(m^3-m)C_1,\\ & [L_m, H_n]=nH_{n+m}-\delta_{m+n, 0}(m^2+m)C_2,\\ &[H_m, H_n]=m\delta_{m+n, 0}C_3,\\ &[L_m,G_p]=(p-\frac m2)G_{p+m}, [L_m, F_p]=(p+\frac m2)F_{m+p},\\ &[G_p, G_q]=-2L_{p+q}+\frac13(p^2-\frac14)\delta_{p+q, 0}C_1,\\ &[G_p, F_q]=H_{p+q}+(2p+1)\delta_{p+q, 0}C_2,\\ &[H_m, G_p]=mF_{m+p}, \ [F_m, F_n]=\delta_{m+n, 0}C_3, \end{align*} $$
$$ \begin{align*} & [L_m,L_n]=(n-m)L_{n+m}+\delta_{m+n, 0}{1\over12}(m^3-m)C_1,\\ & [L_m, H_n]=nH_{n+m}-\delta_{m+n, 0}(m^2+m)C_2,\\ &[H_m, H_n]=m\delta_{m+n, 0}C_3,\\ &[L_m,G_p]=(p-\frac m2)G_{p+m}, [L_m, F_p]=(p+\frac m2)F_{m+p},\\ &[G_p, G_q]=-2L_{p+q}+\frac13(p^2-\frac14)\delta_{p+q, 0}C_1,\\ &[G_p, F_q]=H_{p+q}+(2p+1)\delta_{p+q, 0}C_2,\\ &[H_m, G_p]=mF_{m+p}, \ [F_m, F_n]=\delta_{m+n, 0}C_3, \end{align*} $$
for
![]() $m,n\in {\mathbb Z},\,p, q\in {\mathbb Z}+\frac 12$
.
$m,n\in {\mathbb Z},\,p, q\in {\mathbb Z}+\frac 12$
.
Note that
![]() ${\mathfrak g}$
is equipped with a triangular decomposition and
${\mathfrak g}$
is equipped with a triangular decomposition and
![]() $\frac 12{\mathbb Z}$
-graded structure:
$\frac 12{\mathbb Z}$
-graded structure:
![]() ${{\mathfrak g}}={\mathfrak g}^{+}\oplus \mathfrak g_0\oplus {\mathfrak g}^{-},$
where
${{\mathfrak g}}={\mathfrak g}^{+}\oplus \mathfrak g_0\oplus {\mathfrak g}^{-},$
where
 $$ \begin{align*} &{\mathfrak g}^{\pm}=\bigoplus_{n\in{\mathbb Z}_+, r\in\mathbb N+\frac12}({\mathbb C} L_{\pm n}\oplus{\mathbb C} H_{\pm n}\oplus {\mathbb C} G_{\pm r}\oplus\mathbb CF_{\pm r}),\\ &{\mathfrak g}_0={\mathbb C} H_0\oplus{\mathbb C} L_0\oplus\oplus_{i=1}^3{\mathbb C} C_i. \end{align*} $$
$$ \begin{align*} &{\mathfrak g}^{\pm}=\bigoplus_{n\in{\mathbb Z}_+, r\in\mathbb N+\frac12}({\mathbb C} L_{\pm n}\oplus{\mathbb C} H_{\pm n}\oplus {\mathbb C} G_{\pm r}\oplus\mathbb CF_{\pm r}),\\ &{\mathfrak g}_0={\mathbb C} H_0\oplus{\mathbb C} L_0\oplus\oplus_{i=1}^3{\mathbb C} C_i. \end{align*} $$
Moreover,
is
![]() $\frac 12{\mathbb Z}$
-graded with
$\frac 12{\mathbb Z}$
-graded with
![]() ${\mathfrak g}_i={\mathbb C} L_i\oplus {\mathbb C} H_i$
,
${\mathfrak g}_i={\mathbb C} L_i\oplus {\mathbb C} H_i$
,
![]() ${\mathfrak g}_{r}={\mathbb C} G_{r}\oplus {\mathbb C} F_r$
for
${\mathfrak g}_{r}={\mathbb C} G_{r}\oplus {\mathbb C} F_r$
for
![]() $i\in {\mathbb Z}^*, r\in {\mathbb Z}+\frac 12$
.
$i\in {\mathbb Z}^*, r\in {\mathbb Z}+\frac 12$
.
The
![]() $N=1$
Heisenberg–Virasoro superalgebra
$N=1$
Heisenberg–Virasoro superalgebra
![]() $\mathfrak g$
has a
$\mathfrak g$
has a
![]() $5$
-dimensional canonical Cartan subalgebra
$5$
-dimensional canonical Cartan subalgebra
![]() $\mathfrak h=\mathfrak g_0$
and
$\mathfrak h=\mathfrak g_0$
and
![]() $C_i, i=1,2,3$
with
$C_i, i=1,2,3$
with
![]() $H_0$
span the center of
$H_0$
span the center of
![]() $\mathfrak g$
.
$\mathfrak g$
.
For convenience, we set
Now we consider the following subalgebras of
![]() $\mathfrak g$
:
$\mathfrak g$
:
 $$ \begin{align*} \mathfrak v:&= \mathrm{span}_{\mathbb C} \{L_m, C_1|~ m\in{\mathbb Z}\},\\ \mathfrak{ns}:&= \mathrm{span}_{\mathbb C} \{L_m, G_r, C_1|~ m\in{\mathbb Z}, r\in{\mathbb Z}+\frac12\},\\ \mathfrak{hc}:&= \mathrm{span}_{\mathbb C} \{H_m, F_p, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\},\\ \mathfrak q:&= \mathrm{span}_{\mathbb C} \{L_m, F_p, C_1, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\},\\ \mathfrak p:&= \mathrm{span}_{\mathbb C} \{L_m, H_m, F_p, C_1, C_2, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\}. \end{align*} $$
$$ \begin{align*} \mathfrak v:&= \mathrm{span}_{\mathbb C} \{L_m, C_1|~ m\in{\mathbb Z}\},\\ \mathfrak{ns}:&= \mathrm{span}_{\mathbb C} \{L_m, G_r, C_1|~ m\in{\mathbb Z}, r\in{\mathbb Z}+\frac12\},\\ \mathfrak{hc}:&= \mathrm{span}_{\mathbb C} \{H_m, F_p, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\},\\ \mathfrak q:&= \mathrm{span}_{\mathbb C} \{L_m, F_p, C_1, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\},\\ \mathfrak p:&= \mathrm{span}_{\mathbb C} \{L_m, H_m, F_p, C_1, C_2, C_3\mid m\in{\mathbb Z}, p\in{\mathbb Z}+\frac12\}. \end{align*} $$
Clearly,
![]() $\mathfrak v$
is isomorphic to the Virasoro algebra.
$\mathfrak v$
is isomorphic to the Virasoro algebra.
![]() ${\mathfrak g}_{\bar 0}$
, denoted by
${\mathfrak g}_{\bar 0}$
, denoted by
![]() $\mathfrak t$
for the following use, is isomorphic to the twisted Heisenberg–Virasoro algebra [Reference Arbarello, De Concini, Kac and Procesi3].
$\mathfrak t$
for the following use, is isomorphic to the twisted Heisenberg–Virasoro algebra [Reference Arbarello, De Concini, Kac and Procesi3].
![]() $\mathfrak {ns}$
is isomorphic to the super Virasoro algebra (also called the
$\mathfrak {ns}$
is isomorphic to the super Virasoro algebra (also called the
![]() $N=1$
Neveu-Schwarz algebra, see [Reference Astashkevich4]).
$N=1$
Neveu-Schwarz algebra, see [Reference Astashkevich4]).
![]() $\mathfrak q$
is the Ferminon-Virasoro superalgebra defined in [Reference Xue and Zhao24] (also see [Reference Dilxat, Chen and Liu10]). Moreover,
$\mathfrak q$
is the Ferminon-Virasoro superalgebra defined in [Reference Xue and Zhao24] (also see [Reference Dilxat, Chen and Liu10]). Moreover,
![]() $U(\mathfrak g)$
has a natural
$U(\mathfrak g)$
has a natural
![]() $\frac 12{\mathbb Z}$
-gradation and an induced
$\frac 12{\mathbb Z}$
-gradation and an induced
![]() ${\mathbb Z}_2$
-gradation. For homogeneous
${\mathbb Z}_2$
-gradation. For homogeneous
![]() $u\in U(\mathfrak g_-)$
, we denote by
$u\in U(\mathfrak g_-)$
, we denote by
![]() $|u|$
and
$|u|$
and
![]() $\bar u$
the degree of u according as
$\bar u$
the degree of u according as
![]() $\frac 12{\mathbb Z}$
-gradation and
$\frac 12{\mathbb Z}$
-gradation and
![]() ${\mathbb Z}_2$
-gradation, respectively.
${\mathbb Z}_2$
-gradation, respectively.
2.3 Harish-Chandra modules
For any
![]() $\mathfrak g$
-module V and
$\mathfrak g$
-module V and
![]() $\lambda \in {\mathbb C}$
, set
$\lambda \in {\mathbb C}$
, set
![]() $V_{\lambda }:=\bigl \{v\in V\bigm |L_0v=\lambda v\bigr \}$
, which is generally called the weight space of V corresponding to the weight
$V_{\lambda }:=\bigl \{v\in V\bigm |L_0v=\lambda v\bigr \}$
, which is generally called the weight space of V corresponding to the weight
![]() $\lambda $
. a
$\lambda $
. a
![]() $\mathfrak g$
-module V is called a weight module if V is the sum of all its weight spaces.
$\mathfrak g$
-module V is called a weight module if V is the sum of all its weight spaces.
For a weight module
![]() $V=V_{\bar 0}+V_{\bar 1}$
, we define
$V=V_{\bar 0}+V_{\bar 1}$
, we define
Obviously, if V is a simple weight
![]() $\mathfrak g$
-module, then there exists
$\mathfrak g$
-module, then there exists
![]() $\lambda \in {\mathbb C}$
such that
$\lambda \in {\mathbb C}$
such that
![]() $\mathrm { Supp}(V)\subset \lambda +\frac 12{\mathbb Z}$
. So
$\mathrm { Supp}(V)\subset \lambda +\frac 12{\mathbb Z}$
. So
![]() $V=\sum _{i\in \frac 12{\mathbb Z}}V_i$
is
$V=\sum _{i\in \frac 12{\mathbb Z}}V_i$
is
![]() $\frac 12{\mathbb Z}$
-graded, where
$\frac 12{\mathbb Z}$
-graded, where
![]() $V_i=V_{\lambda +i}$
. An simple weight
$V_i=V_{\lambda +i}$
. An simple weight
![]() $\mathfrak g$
-module
$\mathfrak g$
-module
![]() $V=\sum V_i$
is called Harish-Chandra module if all
$V=\sum V_i$
is called Harish-Chandra module if all
![]() $V_i$
are finite-dimensional. If, in addition, there exists a positive integer N such that
$V_i$
are finite-dimensional. If, in addition, there exists a positive integer N such that
the module V is called cuspidal. If
![]() $N\le 1$
, the cuspidal module V is called intermediate series.
$N\le 1$
, the cuspidal module V is called intermediate series.
A
![]() $\mathfrak g$
-module V is called a highest (resp. lowest) weight module, if there exists a nonzero
$\mathfrak g$
-module V is called a highest (resp. lowest) weight module, if there exists a nonzero
![]() $v \in V_{\lambda }$
such that
$v \in V_{\lambda }$
such that
1) V is generated by v as
![]() $\mathfrak g$
-module with
$\mathfrak g$
-module with
![]() $L_0w=hw$
and
$L_0w=hw$
and
![]() $Cw=cw$
for some
$Cw=cw$
for some
![]() $h,c\in {\mathbb C}$
;
$h,c\in {\mathbb C}$
;
2)
![]() ${\mathfrak g}_+v=0 $
(resp.
${\mathfrak g}_+v=0 $
(resp.
![]() ${\mathfrak g}_- v=0 $
), where
${\mathfrak g}_- v=0 $
), where
![]() ${\mathfrak g}_+=\sum _{i>0}{\mathfrak g}_i$
,
${\mathfrak g}_+=\sum _{i>0}{\mathfrak g}_i$
,
![]() ${\mathfrak g}_-=\sum _{i<0}{\mathfrak g}_i$
.
${\mathfrak g}_-=\sum _{i<0}{\mathfrak g}_i$
.
Next we define the Verma module, which is a highest weight module. For any
![]() $c_1, c_2, c_3, \lambda , h\in \mathbb {C}$
, let
$c_1, c_2, c_3, \lambda , h\in \mathbb {C}$
, let
![]() $\mathbb {C} \mathbf {1}$
be the one-dimensional module over the subalgebra
$\mathbb {C} \mathbf {1}$
be the one-dimensional module over the subalgebra
![]() $\mathfrak {g}_{+}\oplus \mathfrak {g}_0$
defined by
$\mathfrak {g}_{+}\oplus \mathfrak {g}_0$
defined by
Then we get the induced
![]() $\mathfrak g$
-module, called Verma module:
$\mathfrak g$
-module, called Verma module:
It is well known that the Verma module
![]() $M(\lambda , h, c_1, c_2, c_3)$
has a unique maximal submodule
$M(\lambda , h, c_1, c_2, c_3)$
has a unique maximal submodule
![]() $J(\lambda , h, c_1, c_2, c_3),$
and the corresponding simple quotient module is denoted by
$J(\lambda , h, c_1, c_2, c_3),$
and the corresponding simple quotient module is denoted by
![]() $L(\lambda , h, c_1, c_2, c_3)$
. A nonzero weight vector
$L(\lambda , h, c_1, c_2, c_3)$
. A nonzero weight vector
![]() $u'\in M(\lambda , h, c_1, c_2, c_3)$
is called a singular vector if
$u'\in M(\lambda , h, c_1, c_2, c_3)$
is called a singular vector if
![]() $\mathfrak {g}_{+} u'=0$
. It is clear that
$\mathfrak {g}_{+} u'=0$
. It is clear that
![]() $J(\lambda , h, c_1, c_2, c_3)$
is generated by all homogenous singular vectors in
$J(\lambda , h, c_1, c_2, c_3)$
is generated by all homogenous singular vectors in
![]() $M(\lambda , h, c_1, c_2, c_3)$
not in
$M(\lambda , h, c_1, c_2, c_3)$
not in
![]() $\mathbb {C} \mathbf {1}$
, and that
$\mathbb {C} \mathbf {1}$
, and that
![]() $M(\lambda , h, c_1, c_2, c_3)=L(\lambda , h, c_1, c_2, c_3)$
if and only if
$M(\lambda , h, c_1, c_2, c_3)=L(\lambda , h, c_1, c_2, c_3)$
if and only if
![]() $M(\lambda , h, c_1, c_2, c_3)$
does not contain any other singular vectors besides those in
$M(\lambda , h, c_1, c_2, c_3)$
does not contain any other singular vectors besides those in
![]() $\mathbb {C} \mathbf {1}$
.
$\mathbb {C} \mathbf {1}$
.
For the super Virasoro algebra
![]() $\mathfrak {ns}$
, we can also define the Verma module over
$\mathfrak {ns}$
, we can also define the Verma module over
![]() $\mathfrak {ns}$
by
$\mathfrak {ns}$
by
![]() $ M(\lambda , c_1):=U(\mathfrak {ns})\otimes _{U(\mathfrak {ns}_+\oplus \mathfrak {ns}_0)}\mathbb {C} \mathbf {1}_{\mathfrak {ns}}$
, where
$ M(\lambda , c_1):=U(\mathfrak {ns})\otimes _{U(\mathfrak {ns}_+\oplus \mathfrak {ns}_0)}\mathbb {C} \mathbf {1}_{\mathfrak {ns}}$
, where ![]() and
and ![]() . Certainly,
. Certainly,
![]() $M(\lambda , c_1)$
can be regarded as a
$M(\lambda , c_1)$
can be regarded as a
![]() $\mathfrak g$
-module by trivial action of
$\mathfrak g$
-module by trivial action of
![]() $\mathfrak {hc}$
, denoted it by
$\mathfrak {hc}$
, denoted it by
![]() $M(\lambda , c_1)^{\mathfrak g}$
.
$M(\lambda , c_1)^{\mathfrak g}$
.
From [Reference Astashkevich4] we know that there exist homogeneous elements
such that the unique maximal submodule
![]() $J(\lambda , c_1)$
of Verma module
$J(\lambda , c_1)$
of Verma module
![]() $M(\lambda , c_1)$
can be generated by singular vectors
$M(\lambda , c_1)$
can be generated by singular vectors
![]() $P_1\mathbf {1}_{\mathfrak {ns}}$
and
$P_1\mathbf {1}_{\mathfrak {ns}}$
and
![]() $P_2\mathbf {1}_{\mathfrak {ns}}$
:
$P_2\mathbf {1}_{\mathfrak {ns}}$
:
where
![]() $P_1, P_2$
are unique up to nonzero scalars; moreover,
$P_1, P_2$
are unique up to nonzero scalars; moreover,
![]() $P_1=P_2$
if
$P_1=P_2$
if
![]() $J(\lambda , c_1)$
can be generated by a singular vector and
$J(\lambda , c_1)$
can be generated by a singular vector and
![]() $P_1=P_2=0$
if
$P_1=P_2=0$
if
![]() $M(\lambda , c_1)$
itself is simple.
$M(\lambda , c_1)$
itself is simple.
Meanwhile,
![]() $M(c_3):=U(\mathfrak {hc})\otimes _{U(\mathfrak {hc}_{+}+\mathfrak {hc}_0)}\mathbb {C} \mathbf {1}_{\mathfrak {hc}}$
is the Verma module over the Fermion–Clifford superalgebra
$M(c_3):=U(\mathfrak {hc})\otimes _{U(\mathfrak {hc}_{+}+\mathfrak {hc}_0)}\mathbb {C} \mathbf {1}_{\mathfrak {hc}}$
is the Verma module over the Fermion–Clifford superalgebra
![]() $\mathfrak {hc}$
, where
$\mathfrak {hc}$
, where ![]() and
and ![]() . By constructions in [Reference Kac and Todorov12],
. By constructions in [Reference Kac and Todorov12],
![]() $M(c_3)$
can be lifted as a
$M(c_3)$
can be lifted as a
![]() $\mathfrak g$
-module, denoted it by
$\mathfrak g$
-module, denoted it by
![]() $M(c_3)^{\mathfrak g}$
(also see [Reference Liu, Pei, Xia and Zhao15]).
$M(c_3)^{\mathfrak g}$
(also see [Reference Liu, Pei, Xia and Zhao15]).
Theorem 2.2 [Reference Adamović, Jandrić and Radobolja1, Reference Adamovic, Jandric and Radobolja2]
![]() $(1)$
For
$(1)$
For
![]() $c_3\ne 0$
,
$c_3\ne 0$
, ![]() , and then
, and then
![]() $M(\lambda , h, c_1, c_2, c_3)$
is simple if and only if
$M(\lambda , h, c_1, c_2, c_3)$
is simple if and only if
![]() $M(\lambda -\frac 1{2c_3}h^2+\frac {c_2}{c_3}h, c_1-\frac 32+\frac {12c_2}{c_3})$
is a simple
$M(\lambda -\frac 1{2c_3}h^2+\frac {c_2}{c_3}h, c_1-\frac 32+\frac {12c_2}{c_3})$
is a simple
![]() $\mathfrak {ns}$
-module. If
$\mathfrak {ns}$
-module. If
![]() $M(\lambda , h, c_1, c_2, c_3)$
is not simple, the maximal submodule
$M(\lambda , h, c_1, c_2, c_3)$
is not simple, the maximal submodule
![]() $J=U(\mathfrak g_-)P_1\mathbf {1}_{\mathfrak {ns}}\otimes \mathbf 1_{\mathfrak {hc}}+U(\mathfrak g_-)P_2\mathbf {1}_{\mathfrak {ns}}\otimes \mathbf 1_{\mathfrak {hc}}$
, where
$J=U(\mathfrak g_-)P_1\mathbf {1}_{\mathfrak {ns}}\otimes \mathbf 1_{\mathfrak {hc}}+U(\mathfrak g_-)P_2\mathbf {1}_{\mathfrak {ns}}\otimes \mathbf 1_{\mathfrak {hc}}$
, where
![]() $U(\mathfrak {ns}_-)P_1\mathbf {1}_{\mathfrak {ns}}+U(\mathfrak {ns}_-)P_2\mathbf {1}_{\mathfrak {ns}}$
is the maximal submodule of
$U(\mathfrak {ns}_-)P_1\mathbf {1}_{\mathfrak {ns}}+U(\mathfrak {ns}_-)P_2\mathbf {1}_{\mathfrak {ns}}$
is the maximal submodule of
![]() $M(\lambda -\frac 1{2c_3}h^2+\frac {c_2}{c_3}h, c_1-\frac 32+\frac {12c_2}{c_3})$
given by (2.4).
$M(\lambda -\frac 1{2c_3}h^2+\frac {c_2}{c_3}h, c_1-\frac 32+\frac {12c_2}{c_3})$
given by (2.4).
![]() $(2)$
$(2)$
![]() $M(\lambda , h, c_1, c_2, 0)$
is simple if and only if
$M(\lambda , h, c_1, c_2, 0)$
is simple if and only if
![]() $h+(n+1)c_2\ne 0$
for any
$h+(n+1)c_2\ne 0$
for any
![]() $n\in {\mathbb Z}^*$
. Moreover, if
$n\in {\mathbb Z}^*$
. Moreover, if
![]() $h+(n+1)c_2=0$
for some
$h+(n+1)c_2=0$
for some
![]() $n\in {\mathbb Z}^*$
, then the maximal submodule
$n\in {\mathbb Z}^*$
, then the maximal submodule
![]() $J=U(\mathfrak g_-)P_1\mathbf {1}+U(\mathfrak g_-)P_2\mathbf {1}$
, where
$J=U(\mathfrak g_-)P_1\mathbf {1}+U(\mathfrak g_-)P_2\mathbf {1}$
, where
![]() $P_1, P_2$
are given in [Reference Adamovic, Jandric and Radobolja2] (in many cases,
$P_1, P_2$
are given in [Reference Adamovic, Jandric and Radobolja2] (in many cases,
![]() $P_1=P_2$
).
$P_1=P_2$
).
Clearly, simple highest or lowest weight modules are Harish-Chandra modules.
For the Virasoro algebra
![]() $\mathfrak v$
, the intermediate series module
$\mathfrak v$
, the intermediate series module
![]() ${\mathcal A}_{a,\; b}$
for some
${\mathcal A}_{a,\; b}$
for some
![]() $a, b\in {\mathbb C}$
is given by as follows (see [Reference Kaplansky and Santharoubane13]):
$a, b\in {\mathbb C}$
is given by as follows (see [Reference Kaplansky and Santharoubane13]):
It is well known that ![]() , then we can always suppose that
, then we can always suppose that
![]() $a\not \in {\mathbb Z}$
or
$a\not \in {\mathbb Z}$
or
![]() $a=0$
in
$a=0$
in
![]() ${\mathcal A}_{a,\; b}$
. Moreover, the module
${\mathcal A}_{a,\; b}$
. Moreover, the module
![]() ${\mathcal A}_{a,\; b}$
is simple if
${\mathcal A}_{a,\; b}$
is simple if
![]() $a\notin {\mathbb Z}$
or
$a\notin {\mathbb Z}$
or
![]() $b\ne 0, 1$
. In the opposite case, the module contains two simple subquotients namely the trivial module and
$b\ne 0, 1$
. In the opposite case, the module contains two simple subquotients namely the trivial module and ![]() . It is also clear that
. It is also clear that
![]() ${\mathcal A}_{0,0}$
has
${\mathcal A}_{0,0}$
has
![]() ${\mathbb C} v_0$
as a submodule, and its corresponding quotient is denoted by
${\mathbb C} v_0$
as a submodule, and its corresponding quotient is denoted by
![]() ${\mathcal A}_{0,0}^{\prime }$
. Dually,
${\mathcal A}_{0,0}^{\prime }$
. Dually,
![]() ${\mathcal A}_{0,1}$
has
${\mathcal A}_{0,1}$
has
![]() ${\mathbb C} v_0$
as a quotient module, and its corresponding submodule is isomorphic to
${\mathbb C} v_0$
as a quotient module, and its corresponding submodule is isomorphic to
![]() ${\mathcal A}_{0,0}^{\prime }$
. For convenience, we simply write
${\mathcal A}_{0,0}^{\prime }$
. For convenience, we simply write
![]() ${\mathcal A}_{a,b}^{\prime }={\mathcal A}_{a,b}$
when
${\mathcal A}_{a,b}^{\prime }={\mathcal A}_{a,b}$
when
![]() ${\mathcal A}_{a,b}$
is simple.
${\mathcal A}_{a,b}$
is simple.
All simple Harish-Chandra modules over the Virasoro algebra
![]() $\mathfrak v$
were mainly classified in [Reference Mathieu19].
$\mathfrak v$
were mainly classified in [Reference Mathieu19].
Theorem 2.3 [Reference Mathieu19]
Let V be a simple Harish-Chandra module over the Virasoro algebra
![]() $\mathfrak v$
. Then V is a highest weight module, lowest weight module, or a module of the intermediate series.
$\mathfrak v$
. Then V is a highest weight module, lowest weight module, or a module of the intermediate series.
Based on this classification, all simple Harish-Chandra modules over the twisted Heisenberg–Virasoro algebra
![]() $\mathfrak t$
were also classified.
$\mathfrak t$
were also classified.
Theorem 2.4 [Reference Lü and Zhao17]
Let V be a simple Harish-Chandra module over the twisted Heisenberg–Virasoro algebra
![]() $\mathfrak t$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
$\mathfrak t$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
Remark 2.5 The
![]() $\mathfrak t$
-module of the intermediate series, denoted by
$\mathfrak t$
-module of the intermediate series, denoted by
![]() ${\mathcal A}_{a,\; b,\; c}$
for some
${\mathcal A}_{a,\; b,\; c}$
for some
![]() $a, b, c\in {\mathbb C}$
, was given in [Reference Lü and Zhao17] as follows:
$a, b, c\in {\mathbb C}$
, was given in [Reference Lü and Zhao17] as follows:
Moreover, the module
![]() ${\mathcal A}_{a,\; b,\; c}$
is simple if
${\mathcal A}_{a,\; b,\; c}$
is simple if
![]() $a\notin {\mathbb Z}$
or
$a\notin {\mathbb Z}$
or
![]() $b\ne 0, 1$
or
$b\ne 0, 1$
or
![]() $c\ne 0$
. For convenience, we also use
$c\ne 0$
. For convenience, we also use
![]() ${\mathcal A}_{a, b, c}^{\prime }$
to denote by the simple subquotient of
${\mathcal A}_{a, b, c}^{\prime }$
to denote by the simple subquotient of
![]() ${\mathcal A}_{a, b, c}$
.
${\mathcal A}_{a, b, c}$
.
For the super Virasoro algebra
![]() $\mathfrak {ns}$
, its simple Harish-Chandra modules were classified in [Reference Cai, Liu and Lü7, Reference Cai and Lü8, Reference Su22].
$\mathfrak {ns}$
, its simple Harish-Chandra modules were classified in [Reference Cai, Liu and Lü7, Reference Cai and Lü8, Reference Su22].
Theorem 2.6 [Reference Cai, Liu and Lü7, Reference Cai and Lü8, Reference Su22]
Let V be a simple Harish-Chandra module over the super Virasoro algebra
![]() $\mathfrak {ns}$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
$\mathfrak {ns}$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
The module of the intermediate series over the super Virasoro algebra
![]() $\mathfrak {ns}$
was determined by [Reference Su22] as follows (up to parity-change):
$\mathfrak {ns}$
was determined by [Reference Su22] as follows (up to parity-change):
![]() ${\mathcal S}_{a, b}:=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}}{\mathbb C} y_k$
with
${\mathcal S}_{a, b}:=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}}{\mathbb C} y_k$
with
 $$ \begin{align*} L_nx_i&=(a+bn+i)x_{i+n}, \ L_ny_k=(a+(b-\frac12)n+k)y_{k+n},\\ G_rx_i&=y_{r+i}, \ G_ry_k=(a+k+2r(b-\frac12))x_{r+k}, \end{align*} $$
$$ \begin{align*} L_nx_i&=(a+bn+i)x_{i+n}, \ L_ny_k=(a+(b-\frac12)n+k)y_{k+n},\\ G_rx_i&=y_{r+i}, \ G_ry_k=(a+k+2r(b-\frac12))x_{r+k}, \end{align*} $$
for all
![]() $n, i\in {\mathbb Z}, r, k\in {\mathbb Z}+\frac 12$
, where
$n, i\in {\mathbb Z}, r, k\in {\mathbb Z}+\frac 12$
, where
![]() $a, b\in {\mathbb C}$
.
$a, b\in {\mathbb C}$
.
Moreover,
![]() ${\mathcal S}_{a, b}$
is not simple if and only if
${\mathcal S}_{a, b}$
is not simple if and only if
![]() $a=0, b=1$
or
$a=0, b=1$
or
![]() $a=b=\frac 12$
. We also use
$a=b=\frac 12$
. We also use
![]() ${\mathcal S}_{a,b}^{\prime }$
to denote by the simple subquotient of
${\mathcal S}_{a,b}^{\prime }$
to denote by the simple subquotient of
![]() ${\mathcal S}_{a, b}$
.
${\mathcal S}_{a, b}$
.
The following result plays a key role in classification of Harish-Chandra modules for many Lie superalgebras.
Theorem 2.7 [Reference Dilxat, Chen and Liu10]
Let V be a simple Harish-Chandra module over the Lie superalgebra
![]() $\mathfrak q$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series
$\mathfrak q$
. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series
![]() $\mathcal A_{a, b}^{\prime }$
with the trivial action of
$\mathcal A_{a, b}^{\prime }$
with the trivial action of
![]() $F_r$
for any
$F_r$
for any
![]() $r\in {\mathbb Z}+\frac 12$
.
$r\in {\mathbb Z}+\frac 12$
.
3 Simple cuspidal modules
In order to achieve our main result, we first do such researches for the subalgebra
![]() $\mathfrak p$
. Clearly,
$\mathfrak p$
. Clearly,
![]() ${\mathfrak p}_{\bar 0}$
is isomorphic to the twisted Heisenberg–Virasoro algebra
${\mathfrak p}_{\bar 0}$
is isomorphic to the twisted Heisenberg–Virasoro algebra
![]() $\mathfrak t$
and
$\mathfrak t$
and
![]() ${\mathfrak p}_{\bar 1}=\mathrm {span}_{{\mathbb C}}\{F_r\mid r\in {\mathbb Z}+\frac 12\}$
.
${\mathfrak p}_{\bar 1}=\mathrm {span}_{{\mathbb C}}\{F_r\mid r\in {\mathbb Z}+\frac 12\}$
.
Proposition 3.1 Let V be a simple cuspidal
![]() ${\mathfrak p}$
-module. Then V is a Harish-Chandra module of the intermediate series and
${\mathfrak p}$
-module. Then V is a Harish-Chandra module of the intermediate series and ![]() for some
for some
![]() $a, b, c\in {\mathbb C}$
with
$a, b, c\in {\mathbb C}$
with
![]() $H_mv_i=cv_{m+i}$
,
$H_mv_i=cv_{m+i}$
,
![]() $F_{m+\frac 12}V=0$
for all
$F_{m+\frac 12}V=0$
for all
![]() $m\in {\mathbb Z}$
.
$m\in {\mathbb Z}$
.
Proof Clearly, the subalgebra
![]() $\mathrm {span}\{L_m, F_r, C_1, C_3\mid m\in {\mathbb Z} , r\in {\mathbb Z}+\frac 12\}$
is isomorphic to
$\mathrm {span}\{L_m, F_r, C_1, C_3\mid m\in {\mathbb Z} , r\in {\mathbb Z}+\frac 12\}$
is isomorphic to
![]() ${\mathfrak q}$
. By Theorem 2.7, we can choose a simple
${\mathfrak q}$
. By Theorem 2.7, we can choose a simple
![]() $\mathfrak q$
-module
$\mathfrak q$
-module
![]() $V'$
with
$V'$
with
![]() $F_rV'=0$
for all
$F_rV'=0$
for all
![]() $r\in {\mathbb Z}+\frac 12$
. In this case, we have
$r\in {\mathbb Z}+\frac 12$
. In this case, we have
![]() $V=\mathrm {Ind}_{\mathfrak q}^{\mathfrak p}V'$
. Moreover, we have
$V=\mathrm {Ind}_{\mathfrak q}^{\mathfrak p}V'$
. Moreover, we have
![]() $F_rV=0$
for all
$F_rV=0$
for all
![]() $r\in {\mathbb Z}+\frac 12$
by the definition of
$r\in {\mathbb Z}+\frac 12$
by the definition of
![]() $\mathfrak p$
. Then V is a simple
$\mathfrak p$
. Then V is a simple
![]() $\mathfrak p$
-module if and only if V is a simple
$\mathfrak p$
-module if and only if V is a simple
![]() $\mathfrak t$
-module. So the proposition follows from Theorem 2.4.
$\mathfrak t$
-module. So the proposition follows from Theorem 2.4.
Theorem 3.2 Let V be a simple cuspidal
![]() ${\mathfrak g}$
-module. Then V is a module of the intermediate series.
${\mathfrak g}$
-module. Then V is a module of the intermediate series.
Proof Clearly,
![]() $C_1, C_2, C_3$
act on V as zero’s [Reference Lü and Zhao17]. Now we consider the subalgebra
$C_1, C_2, C_3$
act on V as zero’s [Reference Lü and Zhao17]. Now we consider the subalgebra
![]() ${\mathfrak p}$
of
${\mathfrak p}$
of
![]() $\mathfrak g$
.
$\mathfrak g$
.
By Proposition 3.1, we can choose a simple
![]() ${\mathfrak p}$
-module
${\mathfrak p}$
-module
![]() $U=\sum {\mathbb C} u_i$
of V such that
$U=\sum {\mathbb C} u_i$
of V such that
![]() $H_mu_i=cu_{m+i}$
for all
$H_mu_i=cu_{m+i}$
for all
![]() $m, i\in {\mathbb Z}$
, and
$m, i\in {\mathbb Z}$
, and
![]() $F_rU=0$
for all
$F_rU=0$
for all
![]() $r\in {\mathbb Z}+\frac 12$
. In this case,
$r\in {\mathbb Z}+\frac 12$
. In this case,
![]() $V=\sum _{i\ge 0}G^iU$
, where
$V=\sum _{i\ge 0}G^iU$
, where ![]() , the subspace of
, the subspace of
![]() $\mathfrak g$
.
$\mathfrak g$
.
Case 1.
![]() $c=0$
. In this case,
$c=0$
. In this case,
![]() $H_mU=0$
for all
$H_mU=0$
for all
![]() $m\in {\mathbb Z}$
and then
$m\in {\mathbb Z}$
and then
![]() $H_mV=F_rV=0$
for all
$H_mV=F_rV=0$
for all
![]() $m\in {\mathbb Z}, r\in {\mathbb Z}+\frac 12$
. Then V becomes a simple cuspidal
$m\in {\mathbb Z}, r\in {\mathbb Z}+\frac 12$
. Then V becomes a simple cuspidal
![]() $\mathfrak {ns}$
-module. So it follows by [Reference Cai and Lü8, Reference Su22] directly.
$\mathfrak {ns}$
-module. So it follows by [Reference Cai and Lü8, Reference Su22] directly.
Case 2.
![]() $c\ne 0$
.
$c\ne 0$
.
Now we can suppose that
![]() $GU\ne 0$
(otherwise V is a trivial
$GU\ne 0$
(otherwise V is a trivial
![]() $\mathfrak g$
-module). Set
$\mathfrak g$
-module). Set
![]() $G^0U=U$
and
$G^0U=U$
and
![]() $G^{i+1}U=GG^{i}U$
for all
$G^{i+1}U=GG^{i}U$
for all
![]() $i\ge 0$
. Then
$i\ge 0$
. Then
Moreover,
Since V is cuspidal, there exists
![]() $p\in \mathbb N$
such that
$p\in \mathbb N$
such that
By
![]() $QU=0$
and
$QU=0$
and
![]() $[F_r, G_s]u_i=H_{r+s}u_i=cu_{i+r+s}\ne 0$
, where
$[F_r, G_s]u_i=H_{r+s}u_i=cu_{i+r+s}\ne 0$
, where ![]() , the subspace of
, the subspace of
![]() $\mathfrak g$
, we get
$\mathfrak g$
, we get
![]() $HGU=GU$
and then
$HGU=GU$
and then
![]() $HG^2U=U+G^2U=G^2U$
. By induction, we can get
$HG^2U=U+G^2U=G^2U$
. By induction, we can get
![]() $HG^nU=G^nU$
for any
$HG^nU=G^nU$
for any
![]() $n\in \mathbb N$
.
$n\in \mathbb N$
.
Similarly, by
![]() $QU=0$
and
$QU=0$
and
![]() $[F_r, G_s]u_i=H_{r+s}u_i=cu_{i+r+s}\ne 0$
, we get
$[F_r, G_s]u_i=H_{r+s}u_i=cu_{i+r+s}\ne 0$
, we get
![]() $QGU=U$
and then
$QGU=U$
and then
![]() $GQGU=GU$
. So
$GQGU=GU$
. So
![]() $QG^2U=HGU+GQGU=GU$
. By induction, we can get
$QG^2U=HGU+GQGU=GU$
. By induction, we can get
for any
![]() $n\ge 1$
.
$n\ge 1$
.
If
![]() $p=0$
in (3.3), then
$p=0$
in (3.3), then
![]() $V=U+GU$
and then
$V=U+GU$
and then
![]() $\dim (V_i)_\tau \le 1$
for any
$\dim (V_i)_\tau \le 1$
for any
![]() $i\in {\mathbb Z}$
and
$i\in {\mathbb Z}$
and
![]() $\tau \in {\mathbb Z}_2$
.
$\tau \in {\mathbb Z}_2$
.
If
![]() $p>0$
in (3.3), then we can get
$p>0$
in (3.3), then we can get
![]() $G^{p-1}U=G^{p+1}U$
by (3.4). So we can also get
$G^{p-1}U=G^{p+1}U$
by (3.4). So we can also get
![]() $V=U+GU$
. Then the proposition is obtained.
$V=U+GU$
. Then the proposition is obtained.
By direct calculation, we can get the precise module structure on
![]() $V=U+GU$
as follows (up to parity-change):
$V=U+GU$
as follows (up to parity-change):
![]() $V={\mathcal S}_{a, b, c}:=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}+\frac 12}{\mathbb C} y_k$
with
$V={\mathcal S}_{a, b, c}:=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}+\frac 12}{\mathbb C} y_k$
with
 $$ \begin{align*} L_nx_i&=(a+bn+i)x_{i+n}, \ L_ny_k=(a+(b-\frac12)n+k)y_{k+n},\\ G_rx_i&=y_{r+i}, \ G_ry_k=(a+k+2r(b-\frac12))x_{r+k},\\ H_nx_i&=cx_{n+i}, \ H_ny_k=cy_{n+k},\\ F_rx_i&=0, \ F_ry_k=cx_{r+k}, \end{align*} $$
$$ \begin{align*} L_nx_i&=(a+bn+i)x_{i+n}, \ L_ny_k=(a+(b-\frac12)n+k)y_{k+n},\\ G_rx_i&=y_{r+i}, \ G_ry_k=(a+k+2r(b-\frac12))x_{r+k},\\ H_nx_i&=cx_{n+i}, \ H_ny_k=cy_{n+k},\\ F_rx_i&=0, \ F_ry_k=cx_{r+k}, \end{align*} $$
for all
![]() $n, i\in {\mathbb Z}, r, k\in {\mathbb Z}+\frac 12$
, where
$n, i\in {\mathbb Z}, r, k\in {\mathbb Z}+\frac 12$
, where
![]() $a, b, c\in {\mathbb C}$
.
$a, b, c\in {\mathbb C}$
.
Note that
![]() ${\mathcal S}_{a, b, c}$
is not simple if and only if
${\mathcal S}_{a, b, c}$
is not simple if and only if
![]() $a\in {\mathbb Z}, b=1, c=0$
or
$a\in {\mathbb Z}, b=1, c=0$
or
![]() $a\in {\mathbb Z}+\frac 12, b=\frac 12, c=0$
. If
$a\in {\mathbb Z}+\frac 12, b=\frac 12, c=0$
. If
![]() $a\in {\mathbb Z}$
, then
$a\in {\mathbb Z}$
, then ![]() and
and
![]() ${\mathcal S}_{0, 1, 0}$
has a unique simple submodule
${\mathcal S}_{0, 1, 0}$
has a unique simple submodule
![]() ${\mathcal S}_{0, 1, 0}^{\prime }$
spanned by
${\mathcal S}_{0, 1, 0}^{\prime }$
spanned by ![]() .
.
Moreover, by direct calculation, we can get that ![]() if and only if one of the following holds:
if and only if one of the following holds:
(1)
![]() $a-a'\in {\mathbb Z}, b=b', c=c'$
;
$a-a'\in {\mathbb Z}, b=b', c=c'$
;
(2)
![]() $a\not \in {\mathbb Z}, a-a'\in \frac 12+{\mathbb Z}, b=1, b'=\frac 12$
;
$a\not \in {\mathbb Z}, a-a'\in \frac 12+{\mathbb Z}, b=1, b'=\frac 12$
;
(3)
![]() $a\not \in \frac 12+{\mathbb Z}, a-a'\in \frac 12+{\mathbb Z}, b=\frac 12, b'=1$
.
$a\not \in \frac 12+{\mathbb Z}, a-a'\in \frac 12+{\mathbb Z}, b=\frac 12, b'=1$
.
Especially, if
![]() $a\in {\mathbb Z}+\frac 12$
, then
$a\in {\mathbb Z}+\frac 12$
, then ![]() and
and
![]() ${\mathcal S}_{\frac 12, \frac 12, 0}$
has a unique simple quotient module
${\mathcal S}_{\frac 12, \frac 12, 0}$
has a unique simple quotient module
![]() ${\mathcal S}_{\frac 12, \frac 12, 0}^{\prime } :={\mathcal S}_{\frac 12, \frac 12, 0}/\mathbb Cy_{-\frac 12}$
.
${\mathcal S}_{\frac 12, \frac 12, 0}^{\prime } :={\mathcal S}_{\frac 12, \frac 12, 0}/\mathbb Cy_{-\frac 12}$
.
Let
![]() ${\mathcal S}_{a,b, c}^{\prime } ={\mathcal S}_{a, b, c}$
if
${\mathcal S}_{a,b, c}^{\prime } ={\mathcal S}_{a, b, c}$
if
![]() ${\mathcal S}_{a, b, c}$
is simple and
${\mathcal S}_{a, b, c}$
is simple and
![]() ${\mathcal S}_{0, 1, 0}^{\prime }, {\mathcal S}_{\frac 12, \frac 12, 0}^{\prime }$
be defined as above.
${\mathcal S}_{0, 1, 0}^{\prime }, {\mathcal S}_{\frac 12, \frac 12, 0}^{\prime }$
be defined as above.
4 Simple Harish-Chandra modules
In this section, we shall classify all simple Harish-Chandra modules over the
![]() $N=1$
Heisenberg-Virasoro super algebra. The following result is well known.
$N=1$
Heisenberg-Virasoro super algebra. The following result is well known.
Lemma 4.1 Let M be a Harish-Chandra module over the Virasoro algebra with
![]() $\mathrm {supp}(M)\subseteq \lambda +{\mathbb Z}$
. If for any
$\mathrm {supp}(M)\subseteq \lambda +{\mathbb Z}$
. If for any
![]() $v\in M$
, there exists
$v\in M$
, there exists
![]() $N(v)\in \mathbb N$
such that
$N(v)\in \mathbb N$
such that
![]() $L_iv=0, \forall i\geq N(v)$
, then
$L_iv=0, \forall i\geq N(v)$
, then
![]() $\mathrm {supp}(M)$
is upper bounded.
$\mathrm {supp}(M)$
is upper bounded.
With the previous result, we can easily get the following result.
Theorem 4.2 Let V be a Harish-Chandra module over
![]() $\mathfrak g$
. If V is not a highest and lowest module, then V is uniformly bounded.
$\mathfrak g$
. If V is not a highest and lowest module, then V is uniformly bounded.
Proof It is essentially the same as that of Lemma 4.2 in [Reference Cai, Liu and Lü7].
Fix
![]() $\lambda \in \mathrm {supp}(M)$
. Since M is not cuspidal, there exists
$\lambda \in \mathrm {supp}(M)$
. Since M is not cuspidal, there exists
![]() $k\in \frac 12{\mathbb Z}$
such that
$k\in \frac 12{\mathbb Z}$
such that
![]() $\mathrm {dim}\, M_{-k+\lambda }>2(\mathrm {dim}\, M_\lambda +M_{\lambda +\frac 12}+\mathrm {dim}\, M_{\lambda +1}+M_{\lambda +\frac 32}+\mathrm {dim}\, M_{\lambda +2})$
. Without loss of generality, we may assume that
$\mathrm {dim}\, M_{-k+\lambda }>2(\mathrm {dim}\, M_\lambda +M_{\lambda +\frac 12}+\mathrm {dim}\, M_{\lambda +1}+M_{\lambda +\frac 32}+\mathrm {dim}\, M_{\lambda +2})$
. Without loss of generality, we may assume that
![]() $k\in \mathbb N$
. Then there exists a nonzero element
$k\in \mathbb N$
. Then there exists a nonzero element
![]() $w\in M_{-k+\lambda }$
such that
$w\in M_{-k+\lambda }$
such that
![]() $L_kw=L_{k+1}w=H_{k+2}w=G_{k+\frac 12}w=F_{k+\frac 32}w=0$
. Therefore,
$L_kw=L_{k+1}w=H_{k+2}w=G_{k+\frac 12}w=F_{k+\frac 32}w=0$
. Therefore,
![]() $L_iw=H_iw=G_{i-\frac 12}w=F_{i-\frac 12}w=0$
for all
$L_iw=H_iw=G_{i-\frac 12}w=F_{i-\frac 12}w=0$
for all
![]() $i\geq k^2$
, since
$i\geq k^2$
, since
![]() $[{\mathfrak g}_i,{\mathfrak g}_j]={\mathfrak g }_{i+j}$
.
$[{\mathfrak g}_i,{\mathfrak g}_j]={\mathfrak g }_{i+j}$
.
It is easy to see that
![]() $M'=\{v\in M\,|\, \mathrm {dim}\,\,{\mathfrak g}_+v<\infty \}$
is a nonzero submodule of M, where
$M'=\{v\in M\,|\, \mathrm {dim}\,\,{\mathfrak g}_+v<\infty \}$
is a nonzero submodule of M, where
![]() ${\mathfrak g}_+=\sum \limits _{n\in {\mathbb Z}_+}({\mathbb C} L_n+{\mathbb C} H_n+{\mathbb C} G_{n-\frac 12}+{\mathbb C} F_{n-\frac 12})$
. Hence,
${\mathfrak g}_+=\sum \limits _{n\in {\mathbb Z}_+}({\mathbb C} L_n+{\mathbb C} H_n+{\mathbb C} G_{n-\frac 12}+{\mathbb C} F_{n-\frac 12})$
. Hence,
![]() $M=M'$
. So, Lemma 4.1 tells us that
$M=M'$
. So, Lemma 4.1 tells us that
![]() $\mathrm {supp}(M)$
is upper bounded, that is, M is a highest weight module.
$\mathrm {supp}(M)$
is upper bounded, that is, M is a highest weight module.
Combining with Theorems 3.2 and 4.2 and we get the main result of this paper.
Theorem 4.3 Let V be a simple weight
![]() ${\mathfrak g}$
-module with finite dimensional weight spaces. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
${\mathfrak g}$
-module with finite dimensional weight spaces. Then V is a highest weight module, a lowest weight module, or a module of the intermediate series.
5 Tensor product of weight modules
In this section, we study the tensor product of highest weight modules with intermediate series modules over the
![]() $N=1$
Heisenberg–Virasoro superalgebra.
$N=1$
Heisenberg–Virasoro superalgebra.
Let
![]() $M=M(\lambda , h, c_1, c_2, c_3)$
be the Verma module with highest weight vector
$M=M(\lambda , h, c_1, c_2, c_3)$
be the Verma module with highest weight vector
![]() $\mathbf {1}$
, and
$\mathbf {1}$
, and
![]() ${\mathcal S}_{a, b, c}=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}+\frac 12}{\mathbb C} y_k$
be the module of the intermediate series. Without loss of generality, we may assume that
${\mathcal S}_{a, b, c}=\sum _{i\in {\mathbb Z}}{\mathbb C} x_i+\sum _{k\in {\mathbb Z}+\frac 12}{\mathbb C} y_k$
be the module of the intermediate series. Without loss of generality, we may assume that
![]() $\mathbf {1}\in M_{\bar 0}$
in the following. We will consider the tensor product modules
$\mathbf {1}\in M_{\bar 0}$
in the following. We will consider the tensor product modules
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }$
, and
$M \otimes {\mathcal S}_{a, b, c}^{\prime }$
, and
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
.
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
.
Since M and
![]() ${\mathcal S}_{a, b, c}^{\prime }$
are
${\mathcal S}_{a, b, c}^{\prime }$
are
![]() $L_0$
-diagonalizable, so is
$L_0$
-diagonalizable, so is
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }:$
$M \otimes {\mathcal S}_{a, b, c}^{\prime }:$
where
and
 $$ \begin{align*} &v_{m-n}= \begin{cases} x_{m-n}, & if \quad m-n\in{\mathbb Z},\\ y_{m-n},& if \quad m-n\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
$$ \begin{align*} &v_{m-n}= \begin{cases} x_{m-n}, & if \quad m-n\in{\mathbb Z},\\ y_{m-n},& if \quad m-n\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
Remark 5.1 If M is nontrivial, then
![]() $(M \otimes {\mathcal S}_{a, b, c}^{\prime })_{m+h+a}$
is infinite dimensional for all
$(M \otimes {\mathcal S}_{a, b, c}^{\prime })_{m+h+a}$
is infinite dimensional for all
![]() $ m\in \frac 12{\mathbb Z}$
.
$ m\in \frac 12{\mathbb Z}$
.
Lemma 5.2 The module
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is generated by
$M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is generated by
![]() $\{ \mathbf {1}\otimes v_{k}\mid k\in \frac 12 {\mathbb Z}\}$
.
$\{ \mathbf {1}\otimes v_{k}\mid k\in \frac 12 {\mathbb Z}\}$
.
Proof Note that
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is spanned by
$M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is spanned by
![]() $\{ u\mathbf {1}\otimes v_{k}\mid k\in \frac 12{\mathbb Z}, u\in U(\mathfrak g_-)\}$
, so the lemma holds.
$\{ u\mathbf {1}\otimes v_{k}\mid k\in \frac 12{\mathbb Z}, u\in U(\mathfrak g_-)\}$
, so the lemma holds.
Lemma 5.3
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is reducible for all
$M \otimes {\mathcal S}_{a, b, c}^{\prime }$
is reducible for all
![]() $a,b,c, \lambda , h, c_1, c_2, c_3\in {\mathbb C}$
.
$a,b,c, \lambda , h, c_1, c_2, c_3\in {\mathbb C}$
.
Proof It sufficient to prove that every
![]() $\mathbf {1}\otimes v_k$
generates a proper submodule of
$\mathbf {1}\otimes v_k$
generates a proper submodule of
![]() $M \otimes {\mathcal S}_{a, b, c}^{\prime }$
, where
$M \otimes {\mathcal S}_{a, b, c}^{\prime }$
, where
![]() $\mathbf {1}$
is the highest weight vector of M. Assume that
$\mathbf {1}$
is the highest weight vector of M. Assume that
![]() $M\otimes {\mathcal S}_{a, b, c}^{\prime }$
is cyclic on
$M\otimes {\mathcal S}_{a, b, c}^{\prime }$
is cyclic on
![]() $\mathbf {1}\otimes v_k$
, i.e.,
$\mathbf {1}\otimes v_k$
, i.e.,
Then there must exists
![]() $w\in U(\mathfrak g_-)U(\mathfrak {g}_{+})$
such that
$w\in U(\mathfrak g_-)U(\mathfrak {g}_{+})$
such that
Let
where
![]() $u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}}\in U(\mathfrak {g}_{+})$
is a homogeneous element. Since
$u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}}\in U(\mathfrak {g}_{+})$
is a homogeneous element. Since
we can assume there exists some
![]() $u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}} v_k\neq 0$
. Let
$u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}} v_k\neq 0$
. Let
![]() $ L^{\mathbf {i}} H^{\mathbf {j}} G^{\mathbf {k}} F^{\mathbf {l}} $
be a term in the expression of w such that
$ L^{\mathbf {i}} H^{\mathbf {j}} G^{\mathbf {k}} F^{\mathbf {l}} $
be a term in the expression of w such that
![]() $\mathrm {w}(\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l})$
is maximal. By comparing two sides of
$\mathrm {w}(\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l})$
is maximal. By comparing two sides of
![]() $ \mathbf { 1}\otimes v_{k-\frac 12}=w( \mathbf {1}\otimes v_{k})$
, we have
$ \mathbf { 1}\otimes v_{k-\frac 12}=w( \mathbf {1}\otimes v_{k})$
, we have
Since M is a free
![]() $U(\mathfrak g_-)$
-module, it follows that
$U(\mathfrak g_-)$
-module, it follows that
![]() $u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}} v_k=0$
, which is a contradiction. This completes the proof.
$u_{\mathbf {i}, \mathbf {j}, \mathbf {k}, \mathbf {l}} v_k=0$
, which is a contradiction. This completes the proof.
Theorem 5.4
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is simple if and only if it is cyclic on every vector
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is simple if and only if it is cyclic on every vector
![]() $\mathbf 1\otimes v_{k}$
.
$\mathbf 1\otimes v_{k}$
.
Proof The only if part is trivial.
Assume that
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is cyclic on every
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is cyclic on every
![]() $\mathbf {1}\otimes v_k$
. Let U be a submodule and
$\mathbf {1}\otimes v_k$
. Let U be a submodule and
![]() $0\ne x\in U$
homogenous vector. Then
$0\ne x\in U$
homogenous vector. Then
for some ![]() . We use induction on n to show that there is
. We use induction on n to show that there is
![]() $\mathbf {1}\otimes v_k\in U$
for some
$\mathbf {1}\otimes v_k\in U$
for some
![]() $k\in \frac 12{\mathbb Z}$
.
$k\in \frac 12{\mathbb Z}$
.
Case 1.
![]() $c\ne 0$
.
$c\ne 0$
.
Replacing x with
![]() $ux$
for some
$ux$
for some
![]() $u\in U(\mathfrak {g}_{+})$
if necessary, we may assume that
$u\in U(\mathfrak {g}_{+})$
if necessary, we may assume that
![]() $x_{0}=~{\mathbf 1}$
. Choose n such that
$x_{0}=~{\mathbf 1}$
. Choose n such that
![]() $L_jx_{-i}=G_{j+\frac 12}x_{-i}=H_jx_{-i}=F_{j+\frac 12}x_{-i}=0,\forall j\ge n, i=0, \frac 12, \ldots , s$
. Note that
$L_jx_{-i}=G_{j+\frac 12}x_{-i}=H_jx_{-i}=F_{j+\frac 12}x_{-i}=0,\forall j\ge n, i=0, \frac 12, \ldots , s$
. Note that
![]() ${\mathcal S}_{a, b, c}$
is simple as
${\mathcal S}_{a, b, c}$
is simple as
![]() $(\mathfrak g^{(n)}+\mathfrak {hc}+{\mathbb C} C_2)$
-module. Therefore from Density Lemma [Reference Lü and Zhao17], we may choose some
$(\mathfrak g^{(n)}+\mathfrak {hc}+{\mathbb C} C_2)$
-module. Therefore from Density Lemma [Reference Lü and Zhao17], we may choose some
![]() $u\in U(\mathfrak g^{(n)}+\mathfrak {hc}+{\mathbb C} C_2)$
with
$u\in U(\mathfrak g^{(n)}+\mathfrak {hc}+{\mathbb C} C_2)$
with
![]() $uv_{k+i}=\delta _{0,i}v_{0}$
for all
$uv_{k+i}=\delta _{0,i}v_{0}$
for all
![]() $i=0, \frac 12, \ldots , s$
. Rewrite
$i=0, \frac 12, \ldots , s$
. Rewrite
![]() $u=\sum _i u_iu_i^{\prime }$
with
$u=\sum _i u_iu_i^{\prime }$
with
![]() $u_i\in U(\mathfrak {hc})$
and
$u_i\in U(\mathfrak {hc})$
and
![]() $u_i^{\prime }\in U(\mathfrak g^{(n)})$
. Note that
$u_i^{\prime }\in U(\mathfrak g^{(n)})$
. Note that
For sufficient large l, replacing
![]() $H_jH_i $
with
$H_jH_i $
with
![]() $cH_{i+j}$
in
$cH_{i+j}$
in
![]() $H_lu$
, we obtain
$H_lu$
, we obtain
![]() $u'\in U(\mathfrak g^{(n)})$
with
$u'\in U(\mathfrak g^{(n)})$
with
![]() $u'v_{k+i}=H_luv_{k+i}=c \delta _{0,i}v_{l}, \forall i=0, \frac 12, \ldots , s$
. Now
$u'v_{k+i}=H_luv_{k+i}=c \delta _{0,i}v_{l}, \forall i=0, \frac 12, \ldots , s$
. Now
![]() $0\ne u'\beta =c{\mathbf 1}\otimes v_{l}\in M$
.
$0\ne u'\beta =c{\mathbf 1}\otimes v_{l}\in M$
.
Case 2.
![]() $c=0$
.
$c=0$
.
If
![]() $s=0$
, then
$s=0$
, then
![]() $x=x_0\otimes v_n\in U$
. Assume
$x=x_0\otimes v_n\in U$
. Assume
![]() $s>0$
. Recall that
$s>0$
. Recall that
![]() $F_{j-\frac 12}v_i=0$
for any
$F_{j-\frac 12}v_i=0$
for any
![]() $j\in {\mathbb Z}, i\in \frac 12{\mathbb Z}$
.
$j\in {\mathbb Z}, i\in \frac 12{\mathbb Z}$
.
If
![]() $F_{l-\frac 12}x\ne 0$
for some
$F_{l-\frac 12}x\ne 0$
for some
![]() $l\in {\mathbb Z}_+$
, we have
$l\in {\mathbb Z}_+$
, we have
where
![]() $y_i=F_{l-\frac 12}x_{-i}\in L(\lambda , h, c_1, c_2, c_3)_{-i+l-\frac 12}$
. By inductive hypothesis, now there must be some
$y_i=F_{l-\frac 12}x_{-i}\in L(\lambda , h, c_1, c_2, c_3)_{-i+l-\frac 12}$
. By inductive hypothesis, now there must be some
![]() $\mathbf 1\otimes v_k\in U$
.
$\mathbf 1\otimes v_k\in U$
.
So
![]() $F_{i-\frac 12}x=0$
for any
$F_{i-\frac 12}x=0$
for any
![]() $i\in {\mathbb Z}_+$
. Since
$i\in {\mathbb Z}_+$
. Since
![]() $G_{\frac 12}$
,
$G_{\frac 12}$
,
![]() $G_{\frac 32}$
,
$G_{\frac 32}$
,
![]() $F_{\frac 12}$
generate
$F_{\frac 12}$
generate
![]() $\mathfrak g_+$
, vectors
$\mathfrak g_+$
, vectors
![]() $G_{\frac 12}x$
and
$G_{\frac 12}x$
and
![]() $G_{\frac 32}x$
cannot both equal zero, for otherwise x would be a singular vector in
$G_{\frac 32}x$
cannot both equal zero, for otherwise x would be a singular vector in
![]() $L(\lambda , h, c_1, c_2, c_3)$
other than
$L(\lambda , h, c_1, c_2, c_3)$
other than
![]() $\textbf {1}$
. But now we can follow the proof of [Reference Zhang26, Lemma 3.4] (also see [Reference Radobolja21, Theorem 28]). This completes the proof.
$\textbf {1}$
. But now we can follow the proof of [Reference Zhang26, Lemma 3.4] (also see [Reference Radobolja21, Theorem 28]). This completes the proof.
6 Simplicity of tensor product modules
In this section, we shall consider the simplicity of tensor product modules defined in Section 5.
Let us first introduce an auxiliary module, using the called “shifting technique” in [Reference Chen, Guo and Zhao9].
Lemma 6.1 The vector space
![]() $ {\mathcal V}=L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
can be endowed with a
$ {\mathcal V}=L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
can be endowed with a
![]() $\mathfrak g$
-module structure via
$\mathfrak g$
-module structure via
 $$ \begin{align*} &L_{k}(u\mathbf{1}\otimes t^s)=\begin{cases} ( L_k+a+s+kb-|u|)u\mathbf{1}\otimes t^{s+k}, & if \quad s+|u|\in{\mathbb Z},\\ \left( L_k+a+s+k(b-\frac12)-|u|\right)u\mathbf{1}\otimes t^{s+k}, & if \quad s+|u|\in{\mathbb Z}+\frac12.\end{cases}\\ &H_{k}(u\mathbf{1}\otimes t^s)=( H_k+c)u\mathbf{1}\otimes t^{s+k}, \quad s+|u|\in \frac12{\mathbb Z}.\\ &G_{k+\frac12}(u\mathbf{1}\otimes t^s)= \begin{cases} ( G_{k+\frac12}+(-1)^{\bar u})u\mathbf{1}\otimes t^{s+k+\frac12}, & if \quad s+|u|\in{\mathbb Z},\\ \left( G_{k+\frac12}+(-1)^{\bar u}(a+s+(2k+1)(b-\frac12)-|u|)\right)u\mathbf{1}\otimes t^{s+k+\frac12} ,& if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases}\\ &F_{k+\frac12}(u\mathbf{1}\otimes t^s)= \begin{cases} F_{k+\frac12}u\mathbf{1}\otimes t^{s+k+\frac12}, & if \quad s+|u|\in{\mathbb Z},\\ \left( F_{k+\frac12}+(-1)^{\bar u}c\right)u\mathbf{1}\otimes t^{s+k+\frac12} ,& if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
$$ \begin{align*} &L_{k}(u\mathbf{1}\otimes t^s)=\begin{cases} ( L_k+a+s+kb-|u|)u\mathbf{1}\otimes t^{s+k}, & if \quad s+|u|\in{\mathbb Z},\\ \left( L_k+a+s+k(b-\frac12)-|u|\right)u\mathbf{1}\otimes t^{s+k}, & if \quad s+|u|\in{\mathbb Z}+\frac12.\end{cases}\\ &H_{k}(u\mathbf{1}\otimes t^s)=( H_k+c)u\mathbf{1}\otimes t^{s+k}, \quad s+|u|\in \frac12{\mathbb Z}.\\ &G_{k+\frac12}(u\mathbf{1}\otimes t^s)= \begin{cases} ( G_{k+\frac12}+(-1)^{\bar u})u\mathbf{1}\otimes t^{s+k+\frac12}, & if \quad s+|u|\in{\mathbb Z},\\ \left( G_{k+\frac12}+(-1)^{\bar u}(a+s+(2k+1)(b-\frac12)-|u|)\right)u\mathbf{1}\otimes t^{s+k+\frac12} ,& if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases}\\ &F_{k+\frac12}(u\mathbf{1}\otimes t^s)= \begin{cases} F_{k+\frac12}u\mathbf{1}\otimes t^{s+k+\frac12}, & if \quad s+|u|\in{\mathbb Z},\\ \left( F_{k+\frac12}+(-1)^{\bar u}c\right)u\mathbf{1}\otimes t^{s+k+\frac12} ,& if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
Proof It can be checked by straightforward but tedious calculations.
Lemma 6.2 The
![]() $\mathfrak g$
-module
$\mathfrak g$
-module
![]() $L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b,c}$
is isomorphic to
$L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b,c}$
is isomorphic to
![]() ${\mathcal V}=L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
via the following map: for any
${\mathcal V}=L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
via the following map: for any
![]() $m\in {\mathbb Z}$
,
$m\in {\mathbb Z}$
,
 $$ \begin{align*} f : M\otimes {\mathcal S}_{a, b,c} &\to M \otimes {\mathbb C}[t^{\pm \frac12}]\\u\mathbf{1}\otimes x_m&\mapsto u\mathbf{1}\otimes t^{m+|u|},\\u\mathbf{1}\otimes y_{m+\frac12}&\mapsto u\mathbf{1}\otimes t^{m+\frac12+|u|}, \end{align*} $$
$$ \begin{align*} f : M\otimes {\mathcal S}_{a, b,c} &\to M \otimes {\mathbb C}[t^{\pm \frac12}]\\u\mathbf{1}\otimes x_m&\mapsto u\mathbf{1}\otimes t^{m+|u|},\\u\mathbf{1}\otimes y_{m+\frac12}&\mapsto u\mathbf{1}\otimes t^{m+\frac12+|u|}, \end{align*} $$
for all
![]() $m\in \mathbb {Z}, u\in U(\mathfrak g_-)_{-m}$
.
$m\in \mathbb {Z}, u\in U(\mathfrak g_-)_{-m}$
.
Proof It can be checked directly.
We identify
![]() ${\mathcal V}$
${\mathcal V}$
![]() $(\mathrm {resp}., {\mathcal V}')$
with
$(\mathrm {resp}., {\mathcal V}')$
with
![]() $L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a,b, c}$
$L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a,b, c}$
![]() $(\mathrm {resp}., L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a,b,c}^{\prime })$
in this section.
$(\mathrm {resp}., L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a,b,c}^{\prime })$
in this section.
Clearly,
![]() ${\mathcal V}= L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
is the weight space decomposition, that is
${\mathcal V}= L(\lambda , h, c_1, c_2, c_3)\otimes {\mathbb C}[t^{\pm \frac 12}]$
is the weight space decomposition, that is
Moreover, we see that
![]() ${\mathcal V}'$
is generated by
${\mathcal V}'$
is generated by
![]() $\{ \mathbf {1}\otimes t^s \mid s\in \frac 12{\mathbb Z}\}$
.
$\{ \mathbf {1}\otimes t^s \mid s\in \frac 12{\mathbb Z}\}$
.
For
![]() $k\in \frac 12{\mathbb Z}$
, we define
$k\in \frac 12{\mathbb Z}$
, we define

The proof of Theorem 5.4 actually shows the following result.
Corollary 6.3 Let W be a nontrivial submodule in
![]() $L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b, c}^{\prime }$
, then W contains
$L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b, c}^{\prime }$
, then W contains
![]() $W_k$
for some
$W_k$
for some
![]() $k\in \frac 12{\mathbb Z}$
.
$k\in \frac 12{\mathbb Z}$
.
Lemma 6.4
-
(1)
 $W^{(k)}=\sum _{i\in \frac 12\mathbb N} U(\mathfrak g_-)(w\otimes t^{k+i})$
.
$W^{(k)}=\sum _{i\in \frac 12\mathbb N} U(\mathfrak g_-)(w\otimes t^{k+i})$
. -
(2)
 $W^{(k)}\supset \oplus _{i\ge k} L(\lambda , h, c_1, c_2, c_3)\otimes t^{i}$
.
$W^{(k)}\supset \oplus _{i\ge k} L(\lambda , h, c_1, c_2, c_3)\otimes t^{i}$
. -
(3)
 $L(\lambda , h, c_1, c_2, c_3)\otimes t^{k-\frac 12}=W^{(k)}_{k-\frac 12}\oplus {\mathbb C}(w\otimes t^{k-\frac 12})$
.
$L(\lambda , h, c_1, c_2, c_3)\otimes t^{k-\frac 12}=W^{(k)}_{k-\frac 12}\oplus {\mathbb C}(w\otimes t^{k-\frac 12})$
. -
(4) Suppose that P is a weight vector in
 $U(\mathfrak g_-)$
such that
$U(\mathfrak g_-)$
such that
 $P w\otimes t^{k-\frac 12}\in W^{(k)}_{k-\frac 12}\subset L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b, c}$
, then
$P w\otimes t^{k-\frac 12}\in W^{(k)}_{k-\frac 12}\subset L(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}_{a, b, c}$
, then
 $(U(\mathfrak g_-)P w)\otimes t^{k-\frac 12} \subset W^{(k)}_{k-\frac 12}$
.
$(U(\mathfrak g_-)P w)\otimes t^{k-\frac 12} \subset W^{(k)}_{k-\frac 12}$
.
Proof (1) It follows from
![]() $U(\mathfrak g)(w\otimes t^i)=U(\mathfrak g_-)U(\mathfrak {g}_{+}+\mathfrak {g}_0)(w\otimes t^i)\subset \sum _{j\in {\mathbb Z}_+} U(\mathfrak g_-)(w\otimes t^{i+j})$
.
$U(\mathfrak g)(w\otimes t^i)=U(\mathfrak g_-)U(\mathfrak {g}_{+}+\mathfrak {g}_0)(w\otimes t^i)\subset \sum _{j\in {\mathbb Z}_+} U(\mathfrak g_-)(w\otimes t^{i+j})$
.
(2) Using (1) and Lemma 6.1, by induction on
![]() $s+m$
it is straight forward to prove that
$s+m$
it is straight forward to prove that ![]() for all
for all
![]() $i\ge k$
and
$i\ge k$
and
![]() $j_1,\ldots ,j_s,l_1,\ldots ,l_m\in {\mathbb Z}_+$
.
$j_1,\ldots ,j_s,l_1,\ldots ,l_m\in {\mathbb Z}_+$
.
(3) This follows from (2) and the proof of Lemma 5.3.
(4) Suppose that
![]() $P\in U(\mathfrak g_-)_{-p}, p\in \frac 12{\mathbb Z}_+$
. From (2) and Lemma 6.1, we have
$P\in U(\mathfrak g_-)_{-p}, p\in \frac 12{\mathbb Z}_+$
. From (2) and Lemma 6.1, we have
 $$ \begin{align*} & (L_{-i}P w)\otimes t^{k-1}=L_{-i}(P w\otimes t^{k+i-1})) -(a-m+k-1-ib) (P w)\otimes t^{k-1}\in W^{(k)}_{k-1}, \\ &(H_{-i}P w)\otimes t^{k-1}=H_{-i}(P w\otimes t^{k+i-1}))-cP w\otimes t^{k-1}\in W^{(k)}_{k-1},\forall i\in {\mathbb Z}_+. \end{align*} $$
$$ \begin{align*} & (L_{-i}P w)\otimes t^{k-1}=L_{-i}(P w\otimes t^{k+i-1})) -(a-m+k-1-ib) (P w)\otimes t^{k-1}\in W^{(k)}_{k-1}, \\ &(H_{-i}P w)\otimes t^{k-1}=H_{-i}(P w\otimes t^{k+i-1}))-cP w\otimes t^{k-1}\in W^{(k)}_{k-1},\forall i\in {\mathbb Z}_+. \end{align*} $$
Therefore, we may prove (4) by induction on p.
For any
![]() $s\in \frac 12{\mathbb Z}$
, from Lemma 6.2, similar to
$s\in \frac 12{\mathbb Z}$
, from Lemma 6.2, similar to
![]() $\varphi _s$
in [Reference Chen, Guo and Zhao9], we may define the linear map
$\varphi _s$
in [Reference Chen, Guo and Zhao9], we may define the linear map
![]() $\varphi _s: U(\mathfrak g_-)\to {\mathbb C}$
by
$\varphi _s: U(\mathfrak g_-)\to {\mathbb C}$
by
 $$ \begin{align*} &\varphi_s(\mathbf{1})=1,\\ &\varphi_s(H_{-i}u\mathbf{1})=-c\varphi(u),\\ &\varphi_s(L_{-i}u\mathbf{1})=\begin{cases} -(a+s-ib-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}, \\ -(a+s-i(b-\frac12)-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12, \end{cases} \end{align*} $$
$$ \begin{align*} &\varphi_s(\mathbf{1})=1,\\ &\varphi_s(H_{-i}u\mathbf{1})=-c\varphi(u),\\ &\varphi_s(L_{-i}u\mathbf{1})=\begin{cases} -(a+s-ib-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}, \\ -(a+s-i(b-\frac12)-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12, \end{cases} \end{align*} $$
 $$ \begin{align*} &\varphi_s(G_{-i-\frac12}u\mathbf{1})=\begin{cases} -(-1)^{\bar u}\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}, \\ -(-1)^{\bar u}(a+s-(2i+1)(b-\frac12)-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12, \end{cases}\\ &\varphi_s(F_{-i-\frac12}u\mathbf{1})=\begin{cases} 0, & if \quad s+|u|\in{\mathbb Z}, \\ -(-1)^{\bar u}c\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
$$ \begin{align*} &\varphi_s(G_{-i-\frac12}u\mathbf{1})=\begin{cases} -(-1)^{\bar u}\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}, \\ -(-1)^{\bar u}(a+s-(2i+1)(b-\frac12)-|u|+i)\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12, \end{cases}\\ &\varphi_s(F_{-i-\frac12}u\mathbf{1})=\begin{cases} 0, & if \quad s+|u|\in{\mathbb Z}, \\ -(-1)^{\bar u}c\varphi_s(u), & if \quad s+|u|\in{\mathbb Z}+\frac12. \end{cases} \end{align*} $$
It is clear that
![]() $\varphi _s$
depends only on
$\varphi _s$
depends only on
![]() $a, b, c, s$
.
$a, b, c, s$
.
Lemma 6.5 Let
![]() $P \in U(\mathfrak g_-)$
. Then
$P \in U(\mathfrak g_-)$
. Then
-
(1)
 $Pw \otimes t^n \equiv \varphi _n(P)w\otimes t^n\,\, (\mathrm {mod}\, W^{(n+\frac 12)});$
$Pw \otimes t^n \equiv \varphi _n(P)w\otimes t^n\,\, (\mathrm {mod}\, W^{(n+\frac 12)});$
-
(2)
 $Pw \otimes t^n \in W^{(n+\frac 12)}$
if and only if
$Pw \otimes t^n \in W^{(n+\frac 12)}$
if and only if
 $\varphi _n(P)=0$
.
$\varphi _n(P)=0$
.
Proof The proof for (1) is similar to that of [Reference Chen, Guo and Zhao9, Lemma 8]. Part (2) follows from (1).
For
![]() $a, b, c, \lambda , h, c_1, c_2, c_3\in {\mathbb C}$
, by Lemma 5.3,
$a, b, c, \lambda , h, c_1, c_2, c_3\in {\mathbb C}$
, by Lemma 5.3,
![]() $M(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is always reducible, even if
$M(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
is always reducible, even if
![]() $M(\lambda , h, c_1, c_2, c_3) $
is simple. We will give necessary and sufficient conditions for the simplicity of
$M(\lambda , h, c_1, c_2, c_3) $
is simple. We will give necessary and sufficient conditions for the simplicity of
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
.
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b, c}^{\prime }$
.
Theorem 6.6
![]() $(1)$
If
$(1)$
If
![]() $(a, b, c)\ne (\frac 12, \frac 12, 0)$
, then
$(a, b, c)\ne (\frac 12, \frac 12, 0)$
, then
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b,c}^{\prime }$
is simple as a
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b,c}^{\prime }$
is simple as a
![]() $\mathfrak g$
-module if and only if
$\mathfrak g$
-module if and only if
![]() $(\varphi _s(P_1), \varphi _s(P_2))\ne (0, 0)$
for all
$(\varphi _s(P_1), \varphi _s(P_2))\ne (0, 0)$
for all
![]() $s\in \frac 12{\mathbb Z}$
, where
$s\in \frac 12{\mathbb Z}$
, where
![]() $P_1, P_2$
are given in Theorem 2.2.
$P_1, P_2$
are given in Theorem 2.2.
![]() $(2)$
$(2)$
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}^{\prime }_{\frac 12, \frac 12, 0}$
is simple as a
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}^{\prime }_{\frac 12, \frac 12, 0}$
is simple as a
![]() $\mathfrak g$
-module if and only if
$\mathfrak g$
-module if and only if
![]() $(\varphi _s(P_1), \varphi _s(P_2)) \ne (0, 0)$
for all
$(\varphi _s(P_1), \varphi _s(P_2)) \ne (0, 0)$
for all
![]() $s\in \frac 12{\mathbb Z}\setminus \{-\frac 12\}$
.
$s\in \frac 12{\mathbb Z}\setminus \{-\frac 12\}$
.
Proof (1) By Theorem 5.4 and Lemmas 6.4, 6.5, it is clear that
![]() $L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b,c}^{\prime }$
is simple if and only if
$L(\lambda , h, c_1, c_2, c_3) \otimes {\mathcal S}_{a, b,c}^{\prime }$
is simple if and only if
![]() $J\otimes t^s+W_s^{(s+\frac 12)}=M(\lambda , h, c_1, c_2, c_3)\otimes t^s$
for all
$J\otimes t^s+W_s^{(s+\frac 12)}=M(\lambda , h, c_1, c_2, c_3)\otimes t^s$
for all
![]() $s\in \frac 12{\mathbb Z}$
, where
$s\in \frac 12{\mathbb Z}$
, where
![]() $J=U(\mathfrak g_-)P_1w+U(\mathfrak g_-)P_2w$
is the maximal submodule of
$J=U(\mathfrak g_-)P_1w+U(\mathfrak g_-)P_2w$
is the maximal submodule of
![]() $M(\lambda , h, c_1, c_2, c_3)$
given in Theorem 2.2. It is equivalent to that
$M(\lambda , h, c_1, c_2, c_3)$
given in Theorem 2.2. It is equivalent to that
![]() $(U(\mathfrak g_-)P_1w+U(\mathfrak g_-)P_2w)\otimes t^s\not \subset W_{s}^{(s+\frac 12)}$
for all
$(U(\mathfrak g_-)P_1w+U(\mathfrak g_-)P_2w)\otimes t^s\not \subset W_{s}^{(s+\frac 12)}$
for all
![]() $s\in \frac 12{\mathbb Z}$
, and is equivalent to that
$s\in \frac 12{\mathbb Z}$
, and is equivalent to that
![]() $(\varphi _s(P_1), \varphi _s(P_2))\ne (0, 0)$
for all
$(\varphi _s(P_1), \varphi _s(P_2))\ne (0, 0)$
for all
![]() $s\in \frac 12{\mathbb Z}$
. So the statement (1) follows.
$s\in \frac 12{\mathbb Z}$
. So the statement (1) follows.
(2) It is similar to (1), the only difference is that
![]() $\varphi _{-\frac 12}=0$
.
$\varphi _{-\frac 12}=0$
.
Example 6.7
![]() $(1)$
If
$(1)$
If
![]() $\lambda =h=0$
and
$\lambda =h=0$
and
![]() $c_3\ne 0$
, then J is generated by
$c_3\ne 0$
, then J is generated by
![]() $P_1= P_2=G_{-\frac 12}$
. In this case,
$P_1= P_2=G_{-\frac 12}$
. In this case,
![]() $M(0, 0, c_1, c_2, c_3) \otimes {\mathcal S}^{\prime }_{a, b, c}$
is simple if and only if
$M(0, 0, c_1, c_2, c_3) \otimes {\mathcal S}^{\prime }_{a, b, c}$
is simple if and only if
![]() $\phi _s (G_{-\frac 12})\neq 0$
if and only if
$\phi _s (G_{-\frac 12})\neq 0$
if and only if
![]() $a-b\not \in {\mathbb Z}$
.
$a-b\not \in {\mathbb Z}$
.
![]() $(2)$
If
$(2)$
If
![]() $c_3=0, h=-2c_2\ne 0$
, then J is generated by
$c_3=0, h=-2c_2\ne 0$
, then J is generated by
![]() $P_1=H_{-1}\mathbf {1}$
and
$P_1=H_{-1}\mathbf {1}$
and
![]() $P_2=F_{-\frac 12}\mathbf {1}$
. In this case,
$P_2=F_{-\frac 12}\mathbf {1}$
. In this case,
![]() $M(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}^{\prime }_{a, b, c}$
is not simple since
$M(\lambda , h, c_1, c_2, c_3)\otimes {\mathcal S}^{\prime }_{a, b, c}$
is not simple since
for all
![]() $s\in \frac 12\mathbb {Z}$
.
$s\in \frac 12\mathbb {Z}$
.
Theorem 6.8 Let
![]() $V(\lambda , h, c_1, c_2, c_3)$
and
$V(\lambda , h, c_1, c_2, c_3)$
and
![]() $V(\lambda ', h', c_1^{\prime }, c^{\prime }_2, c^{\prime }_3)$
be the highest weight
$V(\lambda ', h', c_1^{\prime }, c^{\prime }_2, c^{\prime }_3)$
be the highest weight
![]() $\mathfrak g$
-modules (not-necessarily simple) with highest weight
$\mathfrak g$
-modules (not-necessarily simple) with highest weight
![]() $(\lambda , h, c_1, c_2, c_3)$
and
$(\lambda , h, c_1, c_2, c_3)$
and
![]() $(\lambda ', h', c_1^{\prime }, c^{\prime }_2, c^{\prime }_3)$
, where
$(\lambda ', h', c_1^{\prime }, c^{\prime }_2, c^{\prime }_3)$
, where
![]() $0 \leq \mathfrak {Re} a, \mathfrak {Re} a' <1, b, b'\ne 1$
. Then
$0 \leq \mathfrak {Re} a, \mathfrak {Re} a' <1, b, b'\ne 1$
. Then
if and only if
Proof The ‘if’ part is trivial. We only need to prove the ‘only if’ part.
Assume that
Fix any
![]() $k\in \frac 12\mathbb {Z}$
such that
$k\in \frac 12\mathbb {Z}$
such that
![]() $k\ne -\frac 12$
when
$k\ne -\frac 12$
when
![]() $(a, b,c)=(\frac 12, \frac 12,0)$
. Since
$(a, b,c)=(\frac 12, \frac 12,0)$
. Since
![]() $\sigma (\mathbf {1}\otimes t^k)$
and
$\sigma (\mathbf {1}\otimes t^k)$
and
![]() $\mathbf {1}\otimes t^k$
are of the same weight, we can assume that
$\mathbf {1}\otimes t^k$
are of the same weight, we can assume that
 $$ \begin{align*}\sigma(\mathbf{1}\otimes t^k)= \sum_{i=1}^{r}p_{i, k}\mathbf{1}'\otimes t^l,\end{align*} $$
$$ \begin{align*}\sigma(\mathbf{1}\otimes t^k)= \sum_{i=1}^{r}p_{i, k}\mathbf{1}'\otimes t^l,\end{align*} $$
where
![]() $p_{i, k}$
are homogeneous elements of
$p_{i, k}$
are homogeneous elements of
![]() $U(\mathfrak g_-)$
and
$U(\mathfrak g_-)$
and
Claim 1
![]() $c=c'$
.
$c=c'$
.
For
![]() $k\in \frac 12{\mathbb Z}$
, we have
$k\in \frac 12{\mathbb Z}$
, we have
 $$ \begin{align*} \sigma(H_{0}(\mathbf{1}\otimes t^k))&=c \sigma (\mathbf{1}\otimes t^{k})=H_{0}\sigma(\mathbf{1} \otimes t^k)\\ &=H_{0}( \sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^l )\\ &=c'\sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^{l}. \end{align*} $$
$$ \begin{align*} \sigma(H_{0}(\mathbf{1}\otimes t^k))&=c \sigma (\mathbf{1}\otimes t^{k})=H_{0}\sigma(\mathbf{1} \otimes t^k)\\ &=H_{0}( \sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^l )\\ &=c'\sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^{l}. \end{align*} $$
Then we get
![]() $c=c'$
.
$c=c'$
.
Claim 2
![]() $\lambda =\lambda ', h=h'$
,
$\lambda =\lambda ', h=h'$
,
![]() $a=a'$
and
$a=a'$
and
![]() $b=b'$
.
$b=b'$
.
For
![]() $m,n\in {\mathbb Z}$
,
$m,n\in {\mathbb Z}$
,
![]() $k\in {\mathbb Z}$
, we have
$k\in {\mathbb Z}$
, we have
 $$ \begin{align} &\sigma(L_{m+n+1}(\mathbf{1}\otimes t^k))\nonumber\\ &=( a+k+(m+n+1)b)\sigma(\mathbf{1}\otimes t^{m+n+1+k}), \nonumber\\ &=L_{m+n+1}\sigma(\mathbf{1}\otimes t^k)\nonumber\\ &=L_{m+n+1}( \sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^l)\nonumber\\ &=\sum_{i=1}^{r}(a'+l+(m+n+1)b'-|u|_{i, k})p_{i, k}\mathbf{1}' \otimes t^{m+n+1+l}. \end{align} $$
$$ \begin{align} &\sigma(L_{m+n+1}(\mathbf{1}\otimes t^k))\nonumber\\ &=( a+k+(m+n+1)b)\sigma(\mathbf{1}\otimes t^{m+n+1+k}), \nonumber\\ &=L_{m+n+1}\sigma(\mathbf{1}\otimes t^k)\nonumber\\ &=L_{m+n+1}( \sum_{i=1}^{r}p_{i, k}\mathbf{1}' \otimes t^l)\nonumber\\ &=\sum_{i=1}^{r}(a'+l+(m+n+1)b'-|u|_{i, k})p_{i, k}\mathbf{1}' \otimes t^{m+n+1+l}. \end{align} $$
As the proof of [Reference Chen, Guo and Zhao9, Theorem 2], we get
![]() $\sigma (\mathbf {1}\otimes t^k)=\mathbf {1}'\otimes t^k$
. So
$\sigma (\mathbf {1}\otimes t^k)=\mathbf {1}'\otimes t^k$
. So
![]() $\sigma $
is an isomorphism from
$\sigma $
is an isomorphism from
![]() $V(\lambda , h, c_1, c_2, c_3)$
to
$V(\lambda , h, c_1, c_2, c_3)$
to
![]() $V(\lambda ', h', c_1^{\prime }, c_2^{\prime }, c_3^{\prime })$
. Thus,
$V(\lambda ', h', c_1^{\prime }, c_2^{\prime }, c_3^{\prime })$
. Thus,
![]() $\lambda =\lambda ', h=h'$
. Then by (6.1), we get
$\lambda =\lambda ', h=h'$
. Then by (6.1), we get
![]() $a=a'$
. By (6.2), we get
$a=a'$
. By (6.2), we get
![]() $b=b'$
.
$b=b'$
.