Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:42:53.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Small Amplitude Limit Cycles for Cubic Systems

Published online by Cambridge University Press:  20 November 2018

V. Guíñez ,
E. Sáez  and
I. Szántó
V. Guíñez
Affiliation:
Universidad Técnica Federico Santa María Departamento de Matemática Casilla 110-V, Valparaiso Chile
E. Sáez
Affiliation:
Universidad Técnica Federico Santa Maria Departamento de Matemática Casilla 110-V, Valparaíso Chile
I. Szántó
Affiliation:
Universidad de Chile Facultad de Ciencias Casilla 653, Santiago Chile
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we study the simultaneous generation of limit cycles out of singular points and infinity for the family of cubic planar systems

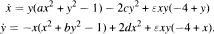
With a suitable choice of parameters, the origin and four other singularities are foci and infinity is a periodic orbit. We prove that it is possible to obtain the following configuration of limit cycles: two small amplitude limit cycles out of the origin, a small amplitude limit cycle out of each of the other four foci, and a large amplitude limit cycle out of infinity. We also obtain other configurations with fewer limit cycles.

Keywords

58F2134C05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 1 , 01 March 1993 , pp. 54 - 63
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Andronov, A. A., et al, Qualitative theory of Second Order Dynamical Systems, Wiley, New York, 1973.Google Scholar
2. Bautin, N. N., On the number of limit cycles which appear with the variation of coefficients, from an equilibrium position of focus or centre type, (In Russian) Mat. Sb. 30(1952), 181–196; Amer. Math. Soc. Transi. Series (1)5(1969), 396–413.Google Scholar
3. Blows, T. R. and Lloyd, N. G., The number of limit cycles of certain polynomial differential equations, Proc. R. Soc. Edinburgh (A) 98(1984), 215–239.Google Scholar
4. Blows, T. R. and Rousseau, C., Bifurcation at infinity in polynomial vector fields, J. Differential Equations, to appear.Google Scholar
5. Guinez, V., Säez, E. and Szántó, I., Limit cycles close to infinity of certain non-linear differential equations, Canad. Math. Bull. (1) 33(1990), 55–59.Google Scholar
6. Guinez, V., Säez, E. and Szanto, I., Simultaneous Hopf bifurcations at the origin and infinity for cubic systems, Proceedings Dynamical Systems, Santiago de Chile, (1990), to appear.Google Scholar
7. James, E. M. and Lloyd, N. G., A cubic system with eight small-amplitude limit cycles, IMA Journal of Applied Mathematics 47(1991), 163–171.Google Scholar
8. Jibin, Li and Qiming, Huang, Bifurcations of limit cycles forming compound eyes in the cubic system, Chin. Ann. of Math. B (4) 8(1987), 391–403.Google Scholar
9. Lloyd, N. G., Blows, T. R. and Kalenge, M. C., Some cubic systems with several limit cycles, Nonlinearity (4) 1(1988), 653–669.Google Scholar
10. Sibirskii, K. S., On the number of limit cycles in the neighborhood of a singular point, Differentsial'nye Uravneniya (1) 1(1965), 53–66.Google Scholar
11. Dongming, Wang, A class of cubic differential systems with 6-tuple focus, Journal of Differential Equations, (2) 87(1990), 305–315.Google Scholar
12. Yan-qian, Ye and Ming-shu, Wang, An important property of the weak focus of a quadratic differential system, Chinese Ann. Math. (A) 4(1983), 65–69; English summary, Chinese Ann. Math. (B) 4(1983), 130.Google Scholar