Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T22:02:46.647Z Has data issue: false hasContentIssue false
  • English
  • Français

A Specialisation of the Bump–Friedberg L-function

Published online by Cambridge University Press:  20 November 2018

Nadir Matringe
Nadir Matringe*
Affiliation:
Université de Poitiers, Laboratoire de Mathématiques et Applications, Téléport 2 - BP 30179, Boulevard Marie et Pierre Curie, 86962, Futuroscope Chasseneuil Cedex e-mail: nadir.matringe@math.univ-poitiers.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the restriction of Bump–Friedberg integrals to affine lines 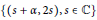$\left\{ \left( s+\alpha ,2s \right),s\in \mathbb{C} \right\}$. It has simple theory, very close to that of the Asai L-function. It is an integral representation of the product 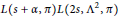$L\left( s+\alpha ,\pi \right)L\left( 2s,{{\Lambda }^{2}},\pi \right)$, which we denote by 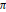${{L}^{\operatorname{lin}}}\left( s,\pi ,\alpha \right)$ for this abstract, when $\pi$ is a cuspidal automorphic representation of 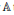$GL\left( k,\mathbb{A} \right)$ for $\mathbb{A}$ the adeles of a number field. When 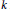$k$ is even, we show that the partial 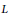$L$-function 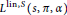${{L}^{\text{lin,S}}}\left( s,\text{ }\!\!\pi\!\!\text{ ,}\alpha \right)$ has a pole at 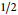$1/2$ if and only if 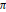$\pi$ admits a (twisted) global period. This gives a more direct proof of a theorem of Jacquet and Friedberg, asserting that π has a twisted global period if and only if 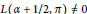$L\left( \alpha +1/2,\text{ }\!\!\pi\!\!\text{ } \right)\ne 0$ and 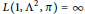$L\left( 1,{{\Lambda }^{2}},\pi \right)=\infty $. When 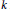$k$ is odd, the partial 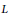$L$-function is holmorphic in a neighbourhood of 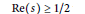$\operatorname{Re}\left( s \right)\ge 1/2$ when 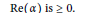$\operatorname{Re}\left( \alpha \right)\,\,\text{is}\,\,\ge \text{0}\,$.

Keywords

11F7011F66automorphic L functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 580 - 595
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Anandavardhanan, U. K., Kable, A. C., and Tandon, R. Distinguished representations and poles of twisted tensor L-functions. Proc. Amer. Math. Soc. 132(2004), no. 10, 2875–2883. http://dx.doi.Org/1 0.1090/S0002-9939-04-07424-6 Google Scholar
[2] Anandavardhanan, U. K. and Rajan, C. S., Distinguished representations, base change, and reducibility for unitary groups. Int. Math. Res. Not. 2005, no. 14, 841–854. http://dx.doi.org/10.1155/IMRN.2005.841 Google Scholar
[3] Ash, A., Ginzburg, D., and Rallis, S., Vanishing periods of cusp forms over modular symbols. Math. Ann. 296(1993), no. 4, 709–723. http://dx.doi.org/10.1007/BF01445131 Google Scholar
[4] Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups. I. Ann. Sci. École Norm. Sup. (4) 10(1977), no. 4, 441–472.Google Scholar
[5] Bump, D. and Friedberg, S., The exterior square automorphic L-functions on GL(«). In: Festschrift in honor of 1.1. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, 1989), Israel Mat h.|Conf. Proc, 3, Weizmann, Jerusalem, 1990, pp. 47–65.Google Scholar
[6] Cogdell, J. W., L-functions and converse theorems for GLB. In: Automorphic forms and applications, IAS/Park City Math. Ser., 12, American Mathematical Society, Providence, RI, 2007, pp. 97–177.Google Scholar
[7] Godement, R. and Jacquet, H., Zeta functions of simple algebras.Lecture Notes in Mathematics, 260, Springer-Verlag, Berlin-New York, 1972.Google Scholar
[8] Flicker, Y. Z., Twisted tensors and Eulerproducts. Bull. Soc. Math. France 116(1988), no. 3, 295–313.Google Scholar
[9] Flicker, Y. Z. and D. Zinoviev, On poles of twisted tensor L-functions. Proc. Japan Acad. Ser. A Math. Sci., 71(1995), no. 6, 114–116. http://dx.doi.Org/10.3792/pjaa.71.114 Google Scholar
[10] Friedberg, S. and Jacquet, H., Linear periods. J. Reine Angew. Math. 443(1993), 91–139. http://dx.doi.Org/1 0.1 51 5/crlU 993.443.91 Google Scholar
[11] Jacquet, H., Piatetski-Shapiro, I.I. and Shalika, J., Automorphic forms on GL(3). II. Ann. of Math. (2) 109(1979), no. 2, 213–258. http://dx.doi.Org/10.2307/1 971112 Google Scholar
[12] Jacquet, H. , Automorphic forms on GL(3). I. Ann. of Math. (2) 109(1979), no. 1,169–212. http://dx.doi.Org/1 0.2307/1 971270 Google Scholar
[13] Jacquet, H. and Rallis, S., Uniqueness of linear periods. Compositio Math. 102(1996), no. 1, 65–123.Google Scholar
[14] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558. http://dx.doi.Org/10.2307/2374103 Google Scholar
[15] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic forms. IL Amer. J. Math. 103(1981), no. 4, 777–815. http://dx.doi.Org/10.2307/2374050 Google Scholar
[16] Jacquet, H. and Shalika, J. A., Exterior square L-functions. In: Automorphic forms, Shimura varieties, and L-functions, Vol. II (Ann Arbor, MI, 1988), Perspect. Math., 11, Academic Press, Boston, MA, 1990, pp. 143–226.Google Scholar
[17] Kable, A. C., Asai L-functions andjacquet's conjecture. Amer. J. Math. 126(2004), no. 4, 789–820. http://dx.doi.org/10.1353/ajm.2004.0030 Google Scholar
[18] Macdonald, I. G., Symmetric functions and Hall polynomials.Second éd.,Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar
[19] Matringe, N., Distinguished representations and exceptional poles of the Asai-L-function. ManuscriptaMath. 131(2010), no. 3-4, 415–426. http://dx.doi.org/10.1007/s00229-009-0327-7 Google Scholar
[20] Matringe, N., Conjectures about distinction and local Asai L-functions. Int. Math. Res. Not. IMRN, 2009, no. 9, 1699–1741. http://dx.doi.Org/10.1 093/imrn/rnp002 Google Scholar
[21] Matringe, N., Distinguished generic representations ofGL(n) over p-adic fields. Int. Math. Res. Not. IMRN 2011, no. 1, 74–95. http://dx.doi.Org/10.1 093/imrn/rnq058 Google Scholar
[22] Matringe, N., On the local Bump-Friedberg L-function. J. Reine Angew. Math., to appear. http://dx.doi.Org/10.1515/crelle-2O13-0083 Google Scholar
[23] Satake, I., Theory of spherical functions on reductive algebraic groups over p-adic fields. Inst. Hautes Études Sci. Publ. Math. 18(1963), 5–69.Google Scholar