Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T20:13:33.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgroup Separability of Generalized Free Products of Free-By-Finite Groups

Published online by Cambridge University Press:  20 November 2018

R. B. J. T. Allenby  and
C. Y. Tang
R. B. J. T. Allenby
Affiliation:
University of Leeds England
C. Y. Tang
Affiliation:
University of Waterloo Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that generalized free products of finitely generated free-byfinite groups amalgamating a cyclic subgroup are subgroup separable. From this it follows that if 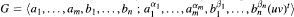where t ≥ 1 and u, v are words on {a1,...,am} and {b1,...,bn} respectively then G is subgroup separable thus generalizing a result in [9] that such groups have solvable word problems.

Keywords

20E0620E2620F0520F10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 4 , 01 December 1993 , pp. 385 - 389
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Allenby, R. B. J. T. and Gregorac, R. J., On locally extended residually finite groups, Conference on Group Theory, Lecture Notes in Math. 319, Springer Verlag, Berlin-Heidelberg-New York, 1973, 9–17.Google Scholar
2. Brunner, A. M., Burns, R. G. and Solitar, D., The subgroup separability of free products of two free groups with cyclic amalgamation, Contemp. Math., Amer. Math. Soc. 33(1984), 90–115.Google Scholar
3. Fine, B. and Rosenberger, G., Generalizing algebraic properties ofFuchsian groups, preprint.Google Scholar
4. Gitik, R., Graphs and lerf groups, preprint.Google Scholar
5. Long, D. D. and Niblo, G. A., Subgroup separability and 3-manifold groups, Math. Z. 207(1991), 209–215.Google Scholar
6. Niblo, G. A., HNN extensions of a free group by Z which are subgroup separable, Proc. London Math. Soc. 61(1990), 18–32.Google Scholar
7. Scott, P., Subgroups of surface groups are almost geometric, J. London Math. Soc. (2) 17(1978), 555–567.Google Scholar
8. Rosenberger, G., Faithful linear representations and residual finitene s s of certain 1 -relator products of cyclics, Siberian Math. J. 32(1991), 203–206.Google Scholar
9. Tang, C. Y., Some results on l-relator quotients of free products, Contemp. Math., Amer. Math. Soc. 109(1990), 165–177.Google Scholar
10. Tang, C. Y., On the subgroup separability of generalized free products of nilpotent groups, Proc. Amer. Math. Soc. 113(1991), 313–318.Google Scholar