Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T01:07:09.615Z Has data issue: false hasContentIssue false
  • English
  • Français

On n-Sums in an Abelian Group

Part of: Abelian groups Sequences and sets Additive number theory; partitions

Published online by Cambridge University Press:  03 November 2015

WEIDONG GAO ,
DAVID J. GRYNKIEWICZ  and
XINGWU XIA
WEIDONG GAO
Affiliation:
Center for Combinatorics, LPMC-TJKLC, Nankai University, Tianjin 300071, PR China (e-mail: wdgao1963@aliyun.com)
DAVID J. GRYNKIEWICZ
Affiliation:
University of Memphis, Memphis, TN 38152, USA (e-mail: diambri@hotmail.com)
XINGWU XIA
Affiliation:
Department of Mathematics, Luoyang Normal University, Luoyang 471022, PR China (e-mail: xxwsjtu@aliyun.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be an additive abelian group, let n ⩾ 1 be an integer, let S be a sequence over G of length |S| ⩾ n + 1, and let 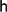${\mathsf h}$(S) denote the maximum multiplicity of a term in S. Let Σn(S) denote the set consisting of all elements in G which can be expressed as the sum of terms from a subsequence of S having length n. In this paper, we prove that either ng ∈ Σn(S) for every term g in S whose multiplicity is at least 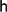${\mathsf h}$(S) − 1 or |Σn(S)| ⩾ min{n + 1, |S| − n + | supp (S)| − 1}, where |supp(S)| denotes the number of distinct terms that occur in S. When G is finite cyclic and n = |G|, this confirms a conjecture of Y. O. Hamidoune from 2003.

MSC classification

Primary: 11B75: Other combinatorial number theory
Secondary: 11P99: None of the above, but in this section 20K01: Finite abelian groups
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 3 , May 2016 , pp. 419 - 435
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bialostocki, A., Grynkiewicz, D. and Lotspeich, M. (2003) On some developments of the Erdős–Ginzburg–Ziv theorem II. Acta Arith. 110 173–184.Google Scholar
[2] Bialostocki, A. and Lotspeich, M. (1992) Some developments of the Erdős–Ginzburg–Ziv theorem. In Sets, Graphs and Numbers, Vol. 60 of Coll. Math. Soc. J. Bolyai, pp. 97–117.Google Scholar
[3] Bollobás, B. and Leader, I. (1999) The number of k-sums modulo k. J. Number Theory 78 27–35.CrossRefGoogle Scholar
[4] Bovey, J. D., Erdős, P. and Niven, I. (1975) Conditions for zero sum modulo n. Canad. Math. Bull. 18 27–29.CrossRefGoogle Scholar
[5] Caro, Y. (1996) Zero-sum problems: A survey. Discrete Math. 152 93–113.Google Scholar
[6] DeVos, M., Goddyn, L. and Mohar, B. (2009) A generalization of Kneser's Addition Theorem. Adv. Math. 220 1531–1548.Google Scholar
[7] Eggleton, R. B. and Erdős, P. (1972) Two combinatorial problems in group theory. Acta Arith. 21 111–116.CrossRefGoogle Scholar
[8] Gallardo, L., Grekos, G. and Pinko, J. (1999) On a variant of the Erdős–Ginzburg–Ziv problem. Acta Arith. 89 331–336.Google Scholar
[9] Gao, W. D. (1995) Addition theorems for finite abelian groups. J. Number Theory 53 241–246.CrossRefGoogle Scholar
[10] Gao, W. D. (1996) A combinatorial problem on finite abelian groups. J. Number Theory 58 100–103.CrossRefGoogle Scholar
[11] Gao, W. D. (1999) On the number of subsequences with given sum. Discrete Math. 195 127–138.CrossRefGoogle Scholar
[12] Gao, W. D. and Leader, I. (2006) Sums and k-sums in abelian groups of order k. J. Number Theory 120 26–32.Google Scholar
[13] Gao, W. D., Li, Y. L., Peng, J. T. and Sun, F. (2008) On subsequence sums of a zero-sum free sequence II. Electron. J. Combin. 15 R117.CrossRefGoogle Scholar
[14] Geroldinger, A. and Halter-Koch, F. (2006) Non-Unique Factorizations: Algebraic, Combinatorial and Analytic Theory, Vol. 278 of Pure and Applied Mathematics, Chapman & Hall/CRC.Google Scholar
[15] Grynkiewicz, D. (2005) On a conjecture of Hamidoune for subsequence sums. Integers 5 A7.Google Scholar
[16] Grynkiewicz, D. (2013) Structural Additive Theory, Developments in Mathematics, Springer.Google Scholar
[17] Grynkiewicz, D. J., Marchan, E. and Ordaz, O. (2009) Representation of finite abelian group elements by subsequence sums. J. Théor. Nombres Bordeaux 21 559–587.CrossRefGoogle Scholar
[18] Hamidoune, Y. O. (2003) Subsequence sums. Combin. Probab. Comput. 12 413–425.Google Scholar
[19] Mann, H. B. (1967) Two addition theorems. J. Combin. Theory 3 233–235.CrossRefGoogle Scholar
[20] Nathanson, M. B. (1996) Additive Number Theory: Inverse Problems and the Geometry of Sumsets, Vol. 165 of Graduate Texts in Mathematics, Springer.Google Scholar
[21] Olson, J. E. (1977) An addition theorem for finite abelian groups. J. Number Theory 9 63–70.Google Scholar
[22] Olson, J. E. and White, E. T. (1977) Sums from a sequence of group elements. In Number Theory and Algebra, Academic Press, pp. 215–222.Google Scholar
[23] Pixton, A. (2009) Sequences with small subsum sets. J. Number Theory 129 806–817.Google Scholar
[24] Savchev, S. and Chen, F. (2008) Long n-zero-free sequences in finite cyclic groups. Discrete Math. 308 1–8.Google Scholar
[25] Scherk, P. (1955) Distinct elements in a set of sums. Amer. Math. Monthly 62 46–47.Google Scholar
[26] Sun, F. (2007) On subsequence sums of a zero-sum free sequence. Electron. J. Combin. 14 R52.CrossRefGoogle Scholar