Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T00:18:18.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Forcing a sparse minor

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  16 April 2015

BRUCE REED  and
DAVID R. WOOD
BRUCE REED
Affiliation:
School of Computer Science, McGill University, Montreal, H3A 0E9, Canada and National Institute of Informatics, Japan (e-mail: breed@cs.mcgill.ca)
DAVID R. WOOD
Affiliation:
School of Mathematical Sciences, Monash University, Melbourne, Victoria 3800, Australia (e-mail: david.wood@monash.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

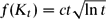This paper addresses the following question for a given graph H: What is the minimum number f(H) such that every graph with average degree at least f(H) contains H as a minor? Due to connections with Hadwiger's conjecture, this question has been studied in depth when H is a complete graph. Kostochka and Thomason independently proved that $f(K_t)=ct\sqrt{\ln t}$. More generally, Myers and Thomason determined f(H) when H has a super-linear number of edges. We focus on the case when H has a linear number of edges. Our main result, which complements the result of Myers and Thomason, states that if H has t vertices and average degree d at least some absolute constant, then 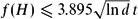$f(H)\leq 3.895\sqrt{\ln d}\,t$. Furthermore, motivated by the case when H has small average degree, we prove that if H has t vertices and q edges, then f(H) ⩽ t + 6.291q (where the coefficient of 1 in the t term is best possible).

MSC classification

Primary: 05C83: Graph minors
Secondary: 05C35: Extremal problems 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 2 , March 2016 , pp. 300 - 322
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Azuma, K. (1967) Weighted sums of certain dependent random variables. Tôhoku Math. J. (2) 19 357–367.CrossRefGoogle Scholar
[2] Bollobás, B., Catlin, P. A. and Erdős, P. (1980) Hadwiger's conjecture is true for almost every graph. European J. Combin. 1 195–199.Google Scholar
[3] Chudnovsky, M., Reed, B. and Seymour, P. (2011) The edge-density for K 2,t minors. J. Combin. Theory Ser. B 101 18–46.CrossRefGoogle Scholar
[4] Corradi, K. and Hajnal, A. (1963) On the maximal number of independent circuits in a graph. Acta Math. Acad. Sci. Hungar. 14 423–443.Google Scholar
[5] Diestel, R. (2010) Graph Theory , fourth edition, Vol. 173 of Graduate Texts in Mathematics, Springer.Google Scholar
[6] Dirac, G. A. (1964) Homomorphism theorems for graphs. Math. Ann. 153 69–80.CrossRefGoogle Scholar
[7] Fernandez de la Vega, W. (1983) On the maximum density of graphs which have no subcontraction to Ks . Discrete Math. 46 109–110.CrossRefGoogle Scholar
[8] Fox, J. and Sudakov, B. (2009) Density theorems for bipartite graphs and related Ramsey-type results. Combinatorica 29 153–196.CrossRefGoogle Scholar
[9] Jørgensen, L. K. (1994) Contractions to K 8. J. Graph Theory 18 431–448.CrossRefGoogle Scholar
[10] Justesen, P. (1989) On independent circuits in finite graphs and a conjecture of Erdős and Pósa. Ann. Discrete Math. 41 299–305.CrossRefGoogle Scholar
[11] Kostochka, A. V. (1982) The minimum Hadwiger number for graphs with a given mean degree of vertices. Metody Diskret. Analiz. 38 37–58.Google Scholar
[12] Kostochka, A. V. (1984) Lower bound of the Hadwiger number of graphs by their average degree. Combinatorica 4 307–316.Google Scholar
[13] Kostochka, A. V. and Prince, N. (2008) On Ks,t -minors in graphs with given average degree. Discrete Math. 308 4435–4445.Google Scholar
[14] Kostochka, A. V. and Prince, N. (2010) Dense graphs have K 3,t minors. Discrete Math. 310 2637–2654.CrossRefGoogle Scholar
[15] Kostochka, A. V. and Prince, N. (2012) On Ks,t -minors in graphs with given average degree, II. Discrete Math. 312 3517–3522.Google Scholar
[16] Kühn, D. and Osthus, D. (2005) Forcing unbalanced complete bipartite minors. European J. Combin. 26 75–81.CrossRefGoogle Scholar
[17] Mader, W. (1967) Homomorphieeigenschaften und mittlere Kantendichte von Graphen. Math. Ann. 174 265–268.CrossRefGoogle Scholar
[18] Mader, W. (1968) Homomorphiesätze für Graphen. Math. Ann. 178 154–168.CrossRefGoogle Scholar
[19] Mader, W. (1972) Existenz n-fach zusammenhängender Teilgraphen in Graphen genügend grosser Kantendichte. Abh. Math. Sem. Univ. Hamburg 37 86–97.Google Scholar
[20] Myers, J. S. (2002) Graphs without large complete minors are quasi-random. Combin. Probab. Comput. 11 571–585.CrossRefGoogle Scholar
[21] Myers, J. S. (2003) The extremal function for unbalanced bipartite minors. Discrete Math. 271 209–222.Google Scholar
[22] Myers, J. S. and Thomason, A. (2005) The extremal function for noncomplete minors. Combinatorica 25 725–753.CrossRefGoogle Scholar
[23] Song, Z. (2004) Extremal Functions for Contractions of Graphs. PhD thesis, Georgia Institute of Technology, USA.Google Scholar
[24] Song, Z. X. and Thomas, R. (2006) The extremal function for K 9 minors. J. Combin. Theory Ser. B 96 240–252.Google Scholar
[25] Thomas, R. and Wollan, P. (2005) An improved linear edge bound for graph linkages. European J. Combin. 26 309–324.Google Scholar
[26] Thomason, A. (1984) An extremal function for contractions of graphs. Math. Proc. Cambridge Philos. Soc. 95 261–265.CrossRefGoogle Scholar
[27] Thomason, A. (2001) The extremal function for complete minors. J. Combin. Theory Ser. B 81 318–338.CrossRefGoogle Scholar
[28] Thomason, A. (2007) Disjoint complete minors and bipartite minors. European J. Combin. 28 1779–1783.Google Scholar
[29] Thomason, A. (2008) Disjoint unions of complete minors. Discrete Math. 308 4370–4377.Google Scholar
[30] Verstraëte, J. (2002) A note on vertex-disjoint cycles. Combin. Probab. Comput. 11 97–102.Google Scholar