Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T08:45:27.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Maxima of Quadratic Boolean Functions

Part of: Graph theory

Published online by Cambridge University Press:  21 December 2015

HUNTER SPINK
HUNTER SPINK*
Affiliation:
Trinity College, Cambridge University, United Kingdom (e-mail: hunterspink@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

How many strict local maxima can a real quadratic function on {0, 1}n have? Holzman conjectured a maximum of 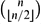$\binom{n }{ \lfloor n/2 \rfloor}$. The aim of this paper is to prove this conjecture. Our approach is via a generalization of Sperner's theorem that may be of independent interest.

MSC classification

Primary: 06E30: Boolean functions
Secondary: 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 4 , July 2016 , pp. 633 - 640
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bollobás, B. (1986) Combinatorics: Set Systems, Hypergraphs, Families of Vectors, and Combinatorial Probability, Cambridge University Press.Google Scholar
[2] Erdős, P. (1945) On a lemma of Littlewood and Offord. Bull. Amer. Math. Soc. 51 898–902.CrossRefGoogle Scholar
[3] Gotsman, C. and Linial, N. (1994) Spectral properties of threshold functions. Combinatorica 14 35–50.CrossRefGoogle Scholar
[4] Kleitman, D. J. (1970) On a lemma of Littlewood and Offord on the distribution of linear combinations of vectors. Adv. Math. 5 251–259.CrossRefGoogle Scholar
[5] O'Donnell, R. (2012) Open problems in analysis of boolean functions. arXiv:1204.6447v1 Google Scholar
[6] Sperner, E. (1928) Ein Satz über Untermenge einer endlichen Menge. Math. Z. 544–548.CrossRefGoogle Scholar