Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T22:19:14.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Turán and Ramsey Properties of Subcube Intersection Graphs

Published online by Cambridge University Press:  03 October 2012

J. ROBERT JOHNSON  and
KLAS MARKSTRÖM
J. ROBERT JOHNSON
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK (e-mail: r.johnson@qmul.ac.uk)
KLAS MARKSTRÖM
Affiliation:
Department of Mathematics and Mathematical Statistics, Umeå University, Umeå 901 87, Sweden (e-mail: klas.markstrom@math.umu.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

The discrete cube {0, 1}d is a fundamental combinatorial structure. A subcube of {0, 1}d is a subset of 2k of its points formed by fixing k coordinates and allowing the remaining d − k to vary freely. This paper is concerned with patterns of intersections among subcubes of the discrete cube. Two sample questions along these lines are as follows: given a family of subcubes in which no r + 1 of them have non-empty intersection, how many pairwise intersections can we have? How many subcubes can we have if among them there are no k which have non-empty intersection and no l which are pairwise disjoint?

These questions are naturally expressed using intersection graphs. The intersection graph of a family of sets has one vertex for each set in the family with two vertices being adjacent if the corresponding subsets intersect. Let 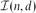$\I(n,d)$ be the set of all n vertex graphs which can be represented as the intersection graphs of subcubes in {0, 1}d. With this notation our first question above asks for the largest number of edges in a Kr+1-free graph in 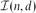$\I(n,d)$. As such it is a Turán-type problem. We answer this question asymptotically for some ranges of r and d. More precisely we show that if $(k+1)2^{\lfloor\frac{d}{k+1}\rfloor}<n\leq k2^{\lfloor\frac{d}{k}\rfloor}$ for some integer k ≥ 2 then the maximum edge density is 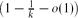$\bigl(1-\frac{1}{k}-o(1)\bigr)$ provided that n is not too close to the lower limit of the range.

The second question can be thought of as a Ramsey-type problem. The maximum such n can be defined in the same way as the usual Ramsey number but only considering graphs which are in 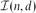$\I(n,d)$. We give bounds for this maximum n mainly concentrating on the case that l is fixed, and make some comparisons with the usual Ramsey number.

Keywords

Primary 05D05Secondary 05C3505C62
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 1 , January 2013 , pp. 55 - 70
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Combin. Theory Ser. A 29 354–360.CrossRefGoogle Scholar
[2]Berg, D. E., Norine, S., Su, F. E., Thomas, R. and Wollan, P. (2010) Voting in agreeable societies. Amer. Math. Monthly 117 27–39.CrossRefGoogle Scholar
[3]Bohman, T. and Keevash, P. (2010) The early evolution of the H-free process. Invent. Math. 181 291–336.CrossRefGoogle Scholar
[4]Bollobás, B. (1998) Modern Graph Theory, Vol. 184 of Graduate Texts in Mathematics, Springer.CrossRefGoogle Scholar
[5]Dénes, J. and Keedwell, A. D. (1974) Latin Squares and their Applications, Academic.Google Scholar
[6]Eckhoff, E. (1988) Intersection properties of boxes I: An upper-bound theorem. Israel J. Math. 62 283–301.CrossRefGoogle Scholar
[7]Erdős, P., Goodman, A. W. and Pósa, L. (1966) The representation of a graph by set intersections. Canad. J. Math. 18 106–112.CrossRefGoogle Scholar
[8]Erdős, P. and Simonovits, M. (1983) Supersaturated graphs and hypergraphs. Combinatorica 3 181–192.CrossRefGoogle Scholar
[9]Graham, R. L., Rothschild, B. L. and Spencer, J. H. (1990) Ramsey Theory, second edition, Wiley-Interscience Series in Discrete Mathematics and Optimization.Google Scholar
[10]Jukna, S. and Kulikov, A. S. (2009) On covering graphs by complete bipartite subgraphs. Discrete Math. 309 3399–3403.CrossRefGoogle Scholar
[11]Kalai, G. (1984) Intersection patterns of convex sets. Israel J. Math. 48 161–174.CrossRefGoogle Scholar
[12]Karoński, M., Scheinerman, E. R. and Singer-Cohen, K. B. (1999) On random intersection graphs: the subgraph problem. Combin. Probab. Comput. 8 131–159.CrossRefGoogle Scholar
[13]Kim, J. H. (1995) The Ramsey number R(3,t) has order of magnitude t 2/log t. Random Struct. Alg. 7 173–207.CrossRefGoogle Scholar
[14]McKee, T. A. and McMorris, F. R. (1999) Topics in Intersection Graph Theory, SIAM Monographs on Discrete Mathematics and Applications.CrossRefGoogle Scholar
[15]Nikiforov, V. (2011) The number of cliques in graphs of given order and size. Trans. Amer. Math. Soc. 363 1599–1618.CrossRefGoogle Scholar
[16]Razborov, A. A. (2008) On the minimal density of triangles in graphs. Combin. Probab. Comput. 17 603–618.CrossRefGoogle Scholar
[17]Roberts, F. S. (1968) On the boxicity and cubicity of a graph. In Recent Progress in Combinatorics: Proc. Third Waterloo Conference on Combinatorics, Academic, pp. 301–310.Google Scholar
[18]Rödl, V. (1985) On a packing and covering problem. Europ. J. Combin. 6 69–78.CrossRefGoogle Scholar
[19]Spencer, J. (1977) Asymptotic lower bounds for Ramsey functions. Discrete Math. 20 69–76.CrossRefGoogle Scholar
[20]Tuza, Z. (1984) Covering of graphs by complete bipartite subgraphs: complexity of 0–1 matrices. Combinatorica 4 111–116.CrossRefGoogle Scholar