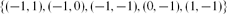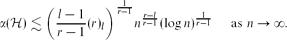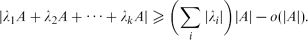Contents
Paper
The Compensation Approach for Walks With Small Steps in the Quarter Plane
-
- Published online by Cambridge University Press:
- 11 January 2013, pp. 161-183
-
- Article
- Export citation
Avoiding Arrays of Odd Order by Latin Squares
-
- Published online by Cambridge University Press:
- 21 December 2012, pp. 184-212
-
- Article
- Export citation
Asymptotic Normality Through Factorial Cumulants and Partition Identities
-
- Published online by Cambridge University Press:
- 21 December 2012, pp. 213-240
-
- Article
- Export citation
On the Independence Number of Steiner Systems
-
- Published online by Cambridge University Press:
- 30 January 2013, pp. 241-252
-
- Article
- Export citation
Expanders Are Universal for the Class of All Spanning Trees
-
- Published online by Cambridge University Press:
- 03 January 2013, pp. 253-281
-
- Article
- Export citation
Sums of Dilates in
 p
p
-
- Published online by Cambridge University Press:
- 30 October 2012, pp. 282-293
-
- Article
- Export citation
Tight Bounds on the Optimization Time of a Randomized Search Heuristic on Linear Functions†
-
- Published online by Cambridge University Press:
- 09 January 2013, pp. 294-318
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 22 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 January 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 22 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 30 January 2013, pp. b1-b6
-
- Article
-
- You have access
- Export citation