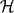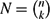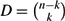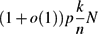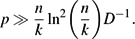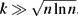Contents
Paper
A Rainbow r-Partite Version of the Erdős–Ko–Rado Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2017, pp. 321-337
-
- Article
- Export citation
Planting Colourings Silently
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 338-366
-
- Article
- Export citation
Stability and Turán Numbers of a Class of Hypergraphs via Lagrangians
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 367-405
-
- Article
- Export citation
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 406-422
-
- Article
- Export citation
Local Conditions for Exponentially Many Subdivisions
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2016, pp. 423-430
-
- Article
- Export citation
On the Number of 4-Edge Paths in Graphs With Given Edge Density
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2016, pp. 431-447
-
- Article
- Export citation
Existence of Spanning ℱ-Free Subgraphs with Large Minimum Degree
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 448-467
-
- Article
- Export citation
An Inequality for Functions on the Hamming Cube
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 468-480
-
- Article
- Export citation