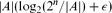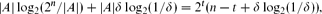Contents
Paper
Modular Orientations of Random and Quasi-Random Regular Graphs
-
- Published online by Cambridge University Press:
- 27 January 2011, pp. 321-329
-
- Article
- Export citation
The Evolution of the Cover Time
-
- Published online by Cambridge University Press:
- 15 February 2011, pp. 331-345
-
- Article
- Export citation
Negative Dependence and Srinivasan's Sampling Process
-
- Published online by Cambridge University Press:
- 22 February 2011, pp. 347-361
-
- Article
- Export citation
Almost Isoperimetric Subsets of the Discrete Cube
-
- Published online by Cambridge University Press:
- 17 February 2011, pp. 363-380
-
- Article
- Export citation
3-Connected Cores In Random Planar Graphs
-
- Published online by Cambridge University Press:
- 24 January 2011, pp. 381-412
-
- Article
- Export citation
Subgraphs of Dense Random Graphs with Specified Degrees
-
- Published online by Cambridge University Press:
- 27 January 2011, pp. 413-433
-
- Article
- Export citation
Asymptotics for First-Passage Times on Delaunay Triangulations
-
- Published online by Cambridge University Press:
- 03 February 2011, pp. 435-453
-
- Article
- Export citation
Szemerédi's Regularity Lemma for Matrices and Sparse Graphs
-
- Published online by Cambridge University Press:
- 03 February 2011, pp. 455-466
-
- Article
- Export citation
The Blind Passenger and the Assignment Problem
-
- Published online by Cambridge University Press:
- 14 February 2011, pp. 467-480
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 20 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 March 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 20 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 March 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation