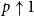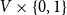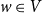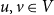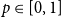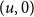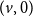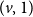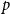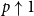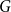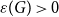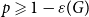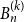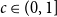Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 4
Detachments of Complete Graphs
-
- Published online by Cambridge University Press:
- 11 April 2005, pp. 275-310
-
- Article
- Export citation
- Cited by 4
The bunkbed conjecture holds in the
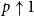 $p\uparrow 1$ limit
$p\uparrow 1$ limit
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2022, pp. 363-369
-
- Article
- Export citation
- Cited by 4
Off-diagonal book Ramsey numbers
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2023, pp. 516-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 4
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 4
Contractible Elements in Graphs and Matroids
-
- Published online by Cambridge University Press:
- 04 July 2003, pp. 457-465
-
- Article
- Export citation
- Cited by 4
Polynomials over structured grids
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
- Cited by 4
Packings in Dense Regular Graphs
-
- Published online by Cambridge University Press:
- 11 April 2005, pp. 325-337
-
- Article
- Export citation
- Cited by 4
On an Online Spanning Tree Problem in Randomly Weighted Graphs
-
- Published online by Cambridge University Press:
- 14 August 2006, pp. 127-144
-
- Article
- Export citation
- Cited by 4
Explicit Constructions of Rödl's Asymptotically Good Packings and Coverings
-
- Published online by Cambridge University Press:
- 01 May 2000, pp. 265-276
-
- Article
- Export citation
- Cited by 4
A Model for Random Random-Walks on Finite Groups
-
- Published online by Cambridge University Press:
- 01 March 1997, pp. 49-56
-
- Article
- Export citation
- Cited by 4
On the Edge Distribution of a Graph
-
- Published online by Cambridge University Press:
- 10 December 2001, pp. 543-555
-
- Article
- Export citation
- Cited by 4
Arithmetic Progressions in Sets with Small Sumsets
-
- Published online by Cambridge University Press:
- 06 March 2006, pp. 597-603
-
- Article
- Export citation
- Cited by 4
A Marstrand Theorem for Subsets of Integers
-
- Published online by Cambridge University Press:
- 25 October 2013, pp. 116-134
-
- Article
- Export citation
- Cited by 4
On Vertices of Degree n in Minimally n-Edge-Connected Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 81-95
-
- Article
- Export citation
- Cited by 4
On a Question of Bourgain about Geometric Incidences
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 619-625
-
- Article
- Export citation
- Cited by 4
Random Matrices and Brownian Motion†
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 157-180
-
- Article
- Export citation
- Cited by 4
Finding an Unknown Acyclic Orientation of a Given Graph
-
- Published online by Cambridge University Press:
- 09 July 2009, pp. 121-131
-
- Article
- Export citation
- Cited by 4
An Inequality for Functions on the Hamming Cube
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 468-480
-
- Article
- Export citation
- Cited by 4
Counting Certain Pairings in Arbitrary Groups
-
- Published online by Cambridge University Press:
- 11 October 2011, pp. 855-865
-
- Article
- Export citation
- Cited by 4
Volumes in the Uniform Infinite Planar Triangulation: From Skeletons to Generating Functions
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 946-973
-
- Article
- Export citation