Kirillov’s orbit method and polynomiality of the faithful dimension of 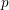$p$-groups

Abstract

Given a finite group 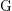$\text{G}$ and a field 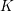$K$, the faithful dimension of 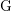$\text{G}$ over 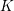$K$ is defined to be the smallest integer $n$ such that 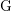$\text{G}$ embeds into 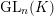$\operatorname{GL}_{n}(K)$. We address the problem of determining the faithful dimension of a 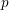$p$-group of the form 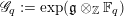$\mathscr{G}_{q}:=\exp (\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$ associated to 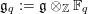$\mathfrak{g}_{q}:=\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$ in the Lazard correspondence, where 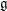$\mathfrak{g}$ is a nilpotent 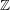$\mathbb{Z}$-Lie algebra which is finitely generated as an abelian group. We show that in general the faithful dimension of 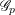$\mathscr{G}_{p}$ is a piecewise polynomial function of 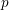$p$ on a partition of primes into Frobenius sets. Furthermore, we prove that for 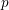$p$ sufficiently large, there exists a partition of 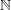$\mathbb{N}$ by sets from the Boolean algebra generated by arithmetic progressions, such that on each part the faithful dimension of 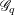$\mathscr{G}_{q}$ for 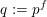$q:=p^{f}$ is equal to 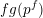$fg(p^{f})$ for a polynomial 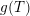$g(T)$. We show that for many naturally arising 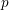$p$-groups, including a vast class of groups defined by partial orders, the faithful dimension is given by a single formula of the latter form. The arguments rely on various tools from number theory, model theory, combinatorics and Lie theory.