Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T08:40:33.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal-dimensional representations of reduced enveloping algebras for 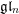$\mathfrak{g}\mathfrak{l}_{n}$

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  11 July 2019

Simon M. Goodwin  and
Lewis Topley
Simon M. Goodwin
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK email s.m.goodwin@bham.ac.uk
Lewis Topley
Affiliation:
School of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, Kent CT2 7FS, UK email L.Topley@kent.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 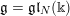$\mathfrak{g}=\mathfrak{g}\mathfrak{l}_{N}(\Bbbk )$, where 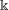$\Bbbk$ is an algebraically closed field of characteristic 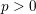$p>0$, and 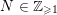$N\in \mathbb{Z}_{{\geqslant}1}$. Let 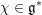$\unicode[STIX]{x1D712}\in \mathfrak{g}^{\ast }$ and denote by 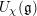$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$ the corresponding reduced enveloping algebra. The Kac–Weisfeiler conjecture, which was proved by Premet, asserts that any finite-dimensional 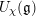$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$-module has dimension divisible by 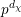$p^{d_{\unicode[STIX]{x1D712}}}$, where 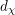$d_{\unicode[STIX]{x1D712}}$ is half the dimension of the coadjoint orbit of 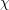$\unicode[STIX]{x1D712}$. Our main theorem gives a classification of 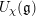$U_{\unicode[STIX]{x1D712}}(\mathfrak{g})$-modules of dimension 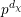$p^{d_{\unicode[STIX]{x1D712}}}$. As a consequence, we deduce that they are all parabolically induced from a one-dimensional module for 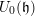$U_{0}(\mathfrak{h})$ for a certain Levi subalgebra 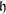$\mathfrak{h}$ of 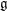$\mathfrak{g}$; we view this as a modular analogue of Mœglin’s theorem on completely primitive ideals in 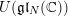$U(\mathfrak{g}\mathfrak{l}_{N}(\mathbb{C}))$. To obtain these results, we reduce to the case where 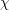$\unicode[STIX]{x1D712}$ is nilpotent, and then classify the one-dimensional modules for the corresponding restricted 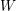$W$-algebra.

Keywords

general linear Lie algebrasreduced enveloping algebrasfinite W-algebrasYangians

MSC classification

Primary: 17B10: Representations, algebraic theory (weights) 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 8 , August 2019 , pp. 1594 - 1617
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bezrukavnikov, R. and Mirkovic, I., Representations of semisimple Lie algebras in prime characteristic and noncommutative Springer resolution , Ann. of Math. (2) 178 (2013), 835–919.Google Scholar
Brundan, J., Mœglin’s theorem and Goldie rank polynomials in Cartan type A , Compos. Math. 147 (2011), 1741–1771.Google Scholar
Brundan, J. and Kleshchev, A., Shifted Yangians and finite W-algebras , Adv. Math. 200 (2006), 136–195.Google Scholar
Brundan, J. and Kleshchev, A., Representations of shifted Yangians and finite W-algebras , Mem. Amer. Math. Soc. 196 (2008), 107.Google Scholar
Brundan, J. and Topley, L., The p-centre of Yangians and shifted Yangians , Mosc. Math. J. 18 (2018), 617–657.Google Scholar
Elashvili, A. G. and Kac, V. G., Classification of good gradings of simple Lie algebras , in Lie groups and invariant theory, American Mathematical Society Translations Series 2, vol. 213, ed. Vinberg, E. B. (American Mathematical Society, Providence, RI, 2005), 85–104.Google Scholar
Friedlander, E. and Parshall, B., Modular representation theory of Lie algebras , Amer. J. Math. 110 (1988), 1055–1093.Google Scholar
Friedlander, E. and Parshall, B., Deformations of Lie algebra representations , Amer. J. Math. 112 (1990), 375–395.Google Scholar
Friedlander, E. and Parshall, B., Induction, deformation, and specialization of Lie algebra representations , Math. Ann. 290 (1991), 473–489.Google Scholar
Goodwin, S. M. and Topley, L., Modular finite W-algebras , Int. Math. Res. Not. IMRN (2018), doi:10.1093/imrn/rnx295.Google Scholar
Humphreys, J. E., Modular representations of simple Lie algebras , Bull. Amer. Math. Soc. (N.S.) 35 (1998), 105–122.Google Scholar
Jantzen, J. C., Representations of Lie algebras in prime characteristic , in Representation theories and algebraic geometry, proceedings, Montreal, NATO ASI Series, vol. C 514, ed. Broer, A. (Kluwer, Dordrecht, 1998), 185–235.Google Scholar
Mœglin, C., Idéaux complètement premiers de l’algèbre enveloppante de gln(ℂ) , J. Algebra 106 (1987), 287–366.Google Scholar
Premet, A., Irreducible representations of Lie algebras of reductive groups and the Kac–Weisfeiler conjecture , Invent. Math. 121 (1995), 79–117.Google Scholar
Premet, A., Special transverse slices and their enveloping algebras , Adv. Math. 170 (2002), 1–55.Google Scholar
Premet, A., Commutative quotients of finite W-algebras , Adv. Math. 225 (2010), 269–306.Google Scholar
Premet, A., Multiplicity-free primitive ideals associated with rigid nilpotent orbits , Transform. Groups 19 (2014), 569–641.Google Scholar
Premet, A. and Topley, L., Derived subalgebras of centralisers and finite W-algebras , Compositio Math. 150 (2014), 1485–1548.Google Scholar
Veisfeiler, B. Yu. and Kats, V. G., Irreducible representations of Lie p-algebras , Funct. Anal. Appl. 5 (1971), 111–117.Google Scholar